Question

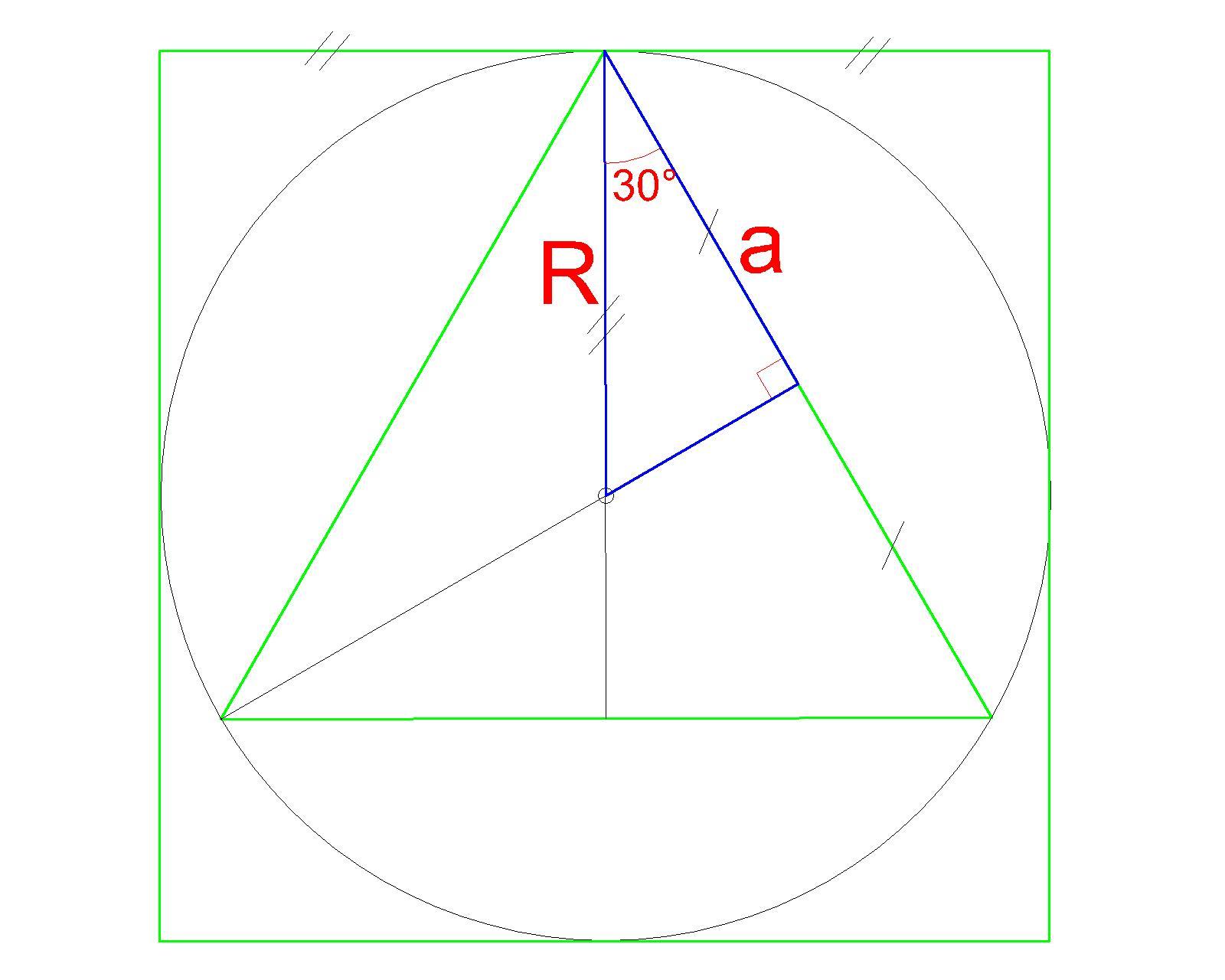
окружность описана около правильного треугольника и вписана в квадрат. Найдите отношение стороны треугольника к стороне квадрата

Answer 1

Ответ:

$frac{2}{sqrt{3}}$

Пошаговое объяснение:

Выполним рисунок.

Связующее звено между треугольником и квадратом - это окружность.

Радиус окружности R равен половине стороны квадрата.

Найдем соотношение радиуса окружности и стороны треугольника.

Внутренние углы правильного треугольника равны по 60°.

Центр описаной окружности находится в точке пересечения высот такого треуогльника. Проведем 2 высоты. Получаем прямоугольный треугольник  с гипотенузой, равной радиусу окружности, катетом, равным половине стороны треугольника и углом между ними 30° (т.к. высота в правильном треугольнике есть и биссектриса и медиана).

По теореме Пифагора найдем половину стороны треугольника:

R = cos 30° * a/2 (где а - сторона треугольника)

$frac{a}{2} =frac{2R}{sqrt{3} }$.

Значит соотношение сторон треугольника и квадрата:

$frac{2R}{Rsqrt{3} } =frac{2}{sqrt{3} }$