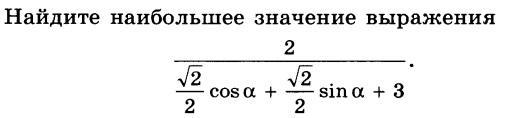Ответы
Ответ дал:
0
Объяснение:
Формула:
sinхcosу+cosхsinу=sin(х+у)
sin45°=cos45°=√2/2
√2/2•cosa+√2/2•sina+3=
=sin45°cosa+cos45°sina+3=3+sin(45°+a)≥2=>
√2/2•cosa+√2/2•sina+3≥2. Т.е. минимум знаменателя равно 2.
Данное выражение принимает наибольшее значение при наименьшем значении знаменателя.
Значить, наибольшее возможное значение равно 2/2=1
Вас заинтересует
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад