Question

Пожалуйста помогите решить срочно

Answer 1

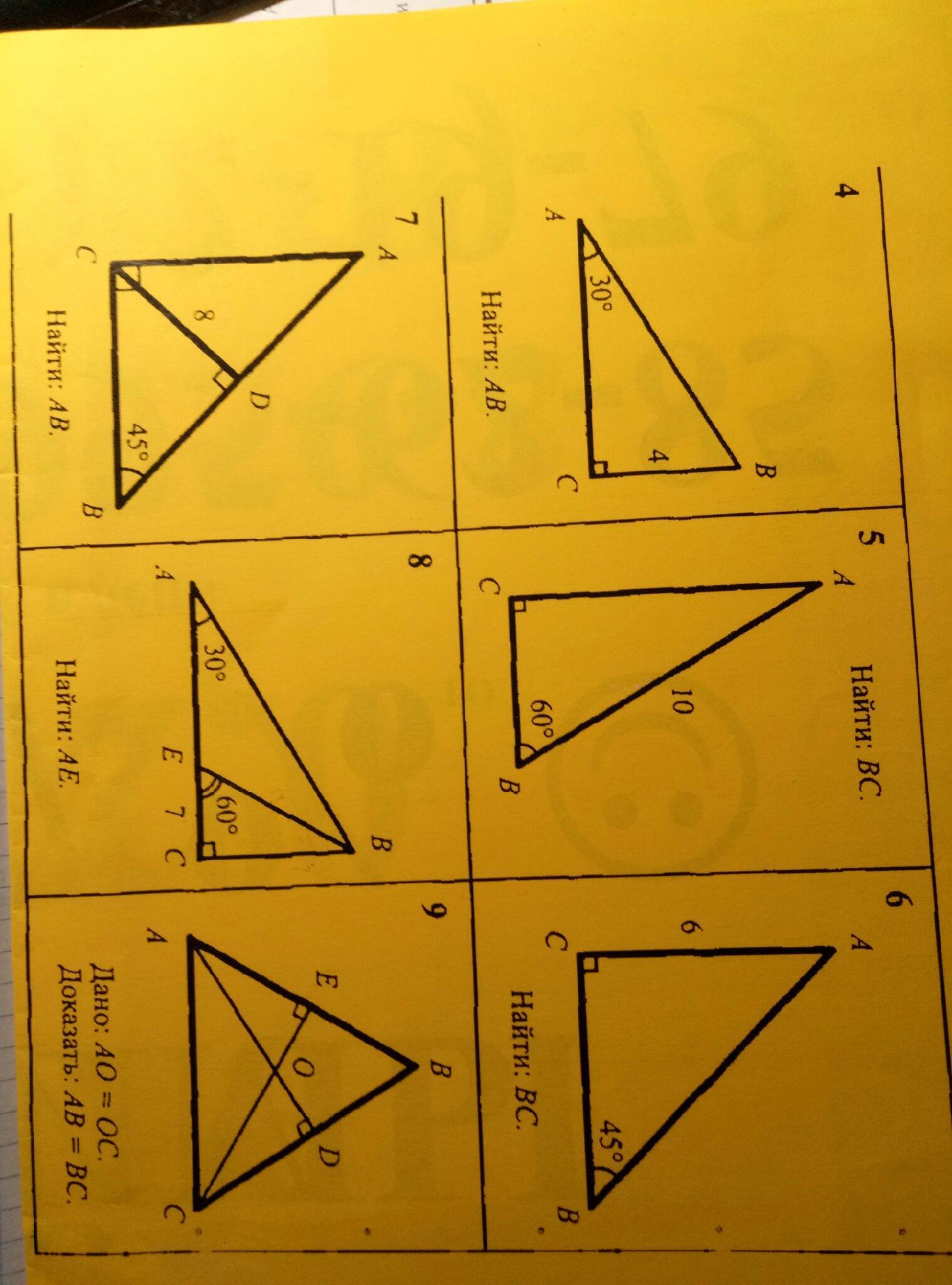
4. Напротив угла 30° лежит катет, равный половине гипотенузы.

$sin30^o=frac{BC}{AB} :=>: AB = frac{BC}{sin30^o}\AB = 4:frac{1}{2}=4cdot frac{1}{2}=8$

5. Здесь то же самое правило про угол 30° и противолежащий катет

$cos60^o=frac{BC}{AB} :=>: BC = ABcdot cos60^o\BC = 10cdot frac{1}{2} = 5$

6. ∠A=∠B= 45° — треугольник равнобедренный, значит AC=BC=6.

Тригонометрическое решение:

$tan45^o=frac{AC}{BC} :=>: BC=frac{AC}{tg45^o} \BC=frac{6}{1} = 6$

7. ∠DCB=∠B=45° ⇒ΔCDB — равнобедренный, CD=DB=8

∠A=∠B=45° ⇒ΔABC — AB=2*DB = 2*8=16

8.

$tg60^o=frac{BC}{EC} :=>: BC=ECcdot tg60^o\BC=7cdot tg60^o = 7 sqrt{3}$

$tg60^o=frac{BC}{EC} :Rightarrow: BC=ECcdot tg60^o\BC=7cdot tg60^o = 7 sqrt{3} \\tg30^o=frac{BC}{AC} :Rightarrow: AC=frac{BC}{tg30^o} \AC=frac{BC}{tg30^o} = 7 sqrt{3} : frac{sqrt{3} }{3} =7 sqrt{3}cdot frac{3}{sqrt{3} }=21\\AE = AC-EC \AE = 21-7=14$

9. AO=OC ⇒ ΔAOC — равнобедренный: ∠CAO=∠OCA.

Рассмотрим прямоугольные треугольники AEC и ADC. У них общая гипотенуза AC и равные острые углы ∠CAD=∠ECA. Следовательно, они равны по гипотенузе и острому углу. Поэтому ∠CAE = ∠DCA как соответствующие углы.

У треугольника ABC равны углы, лежащие против сторон AB и BC, поэтому AB=BC, что и требовалось доказать.