Question

Менша основа і бічні сторони рівнобічної трапеції дорівнюють по 4см. Знайдіть площу трапеції, якщо її тупий кут дорівнює 120 градусів. *
Очень надо пожалуйста!!!!!!

Answer 1

Ответ:

12√3 см².

Объяснение:

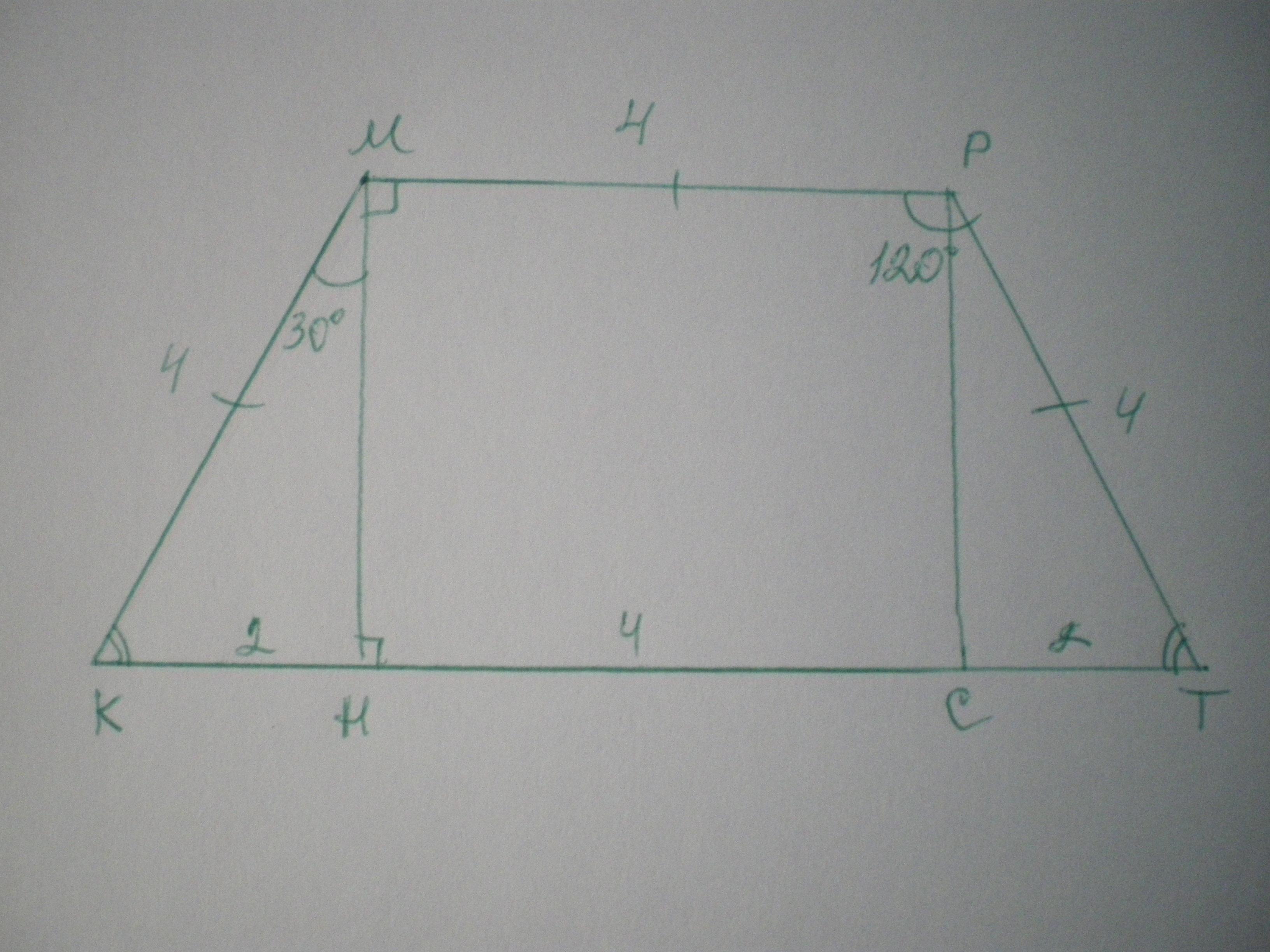
Дано: КМРТ - трапеція, КМ=МР=РТ=4 см, ∠МРТ=∠КМР=120°. Знайти S(КМРТ).

Проведемо висоти МН та РС. ΔКМН=ΔТРС за двома кутами, отже КН=СТ.

∠КМН=120-90=30°, отже КН=1/2 КМ=2 см.  СТ=2 см,  СН=МР=4 см;  

КТ=2+4+2=8 см.

За теоремою Піфагора МН=√(КМ²-КН²)=√(16-4)=√12=2√3 см.

S=(МР+КТ)/2 * МН = (8+4)/2*2√3=12√3 см².

Answer 2

Дякую!