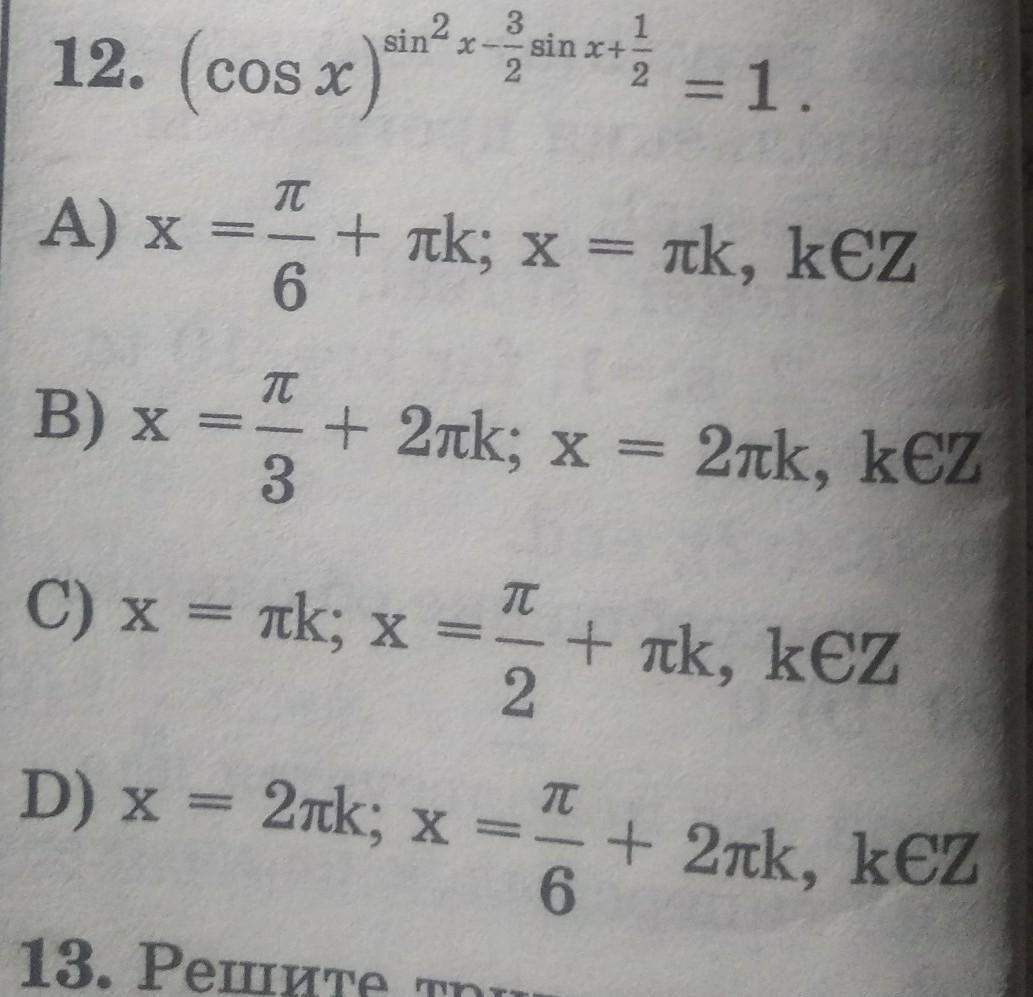Question

помогите решить тригонометрическое уравнение​

Answer 1

Ответ: D

Пошаговое объяснение:

Чтобы косинус в какой-то степени равнялся единице, эта степень должна быть равна нулю:

$sin^2x-frac{3}{2}sinx+frac{1}{2}=0\sinx=t\t^2-frac{3}{2}t+frac{1}{2}=0\2t^2-3t+1=0\t_1=frac{1}{2}\t_2=1$

Первый случай:

$sin(x_1)=frac{1}{2}\x_1=frac{pi}{6} +2pi k , k in Z\\x_1=frac{5pi}{6} +2pi k , k in Z$

Второй случай:

$sin(x_2)=1\x_2=frac{pi}{2} +2pi k , k in Z$

Однако это не все. Еще есть вариант, когда $cosx=1$. Тогда в какой бы степени ни находилась единица, она все равно останется единицей:

$cosx=1\x=2pi k, k in Z$

Объединив решения, найдем подходящий вариант ответа:

Ответ D.