три окружности с радиусами 2,3,9 касаются попарно внешним образом. определить периметр треугольника с вершинами в центрах этих окружностей
Приложения:

Ответы
Ответ дал:
0
Ответ:
PΔ = (2+2)+(3+3)+(9+9) = 28
Объяснение:
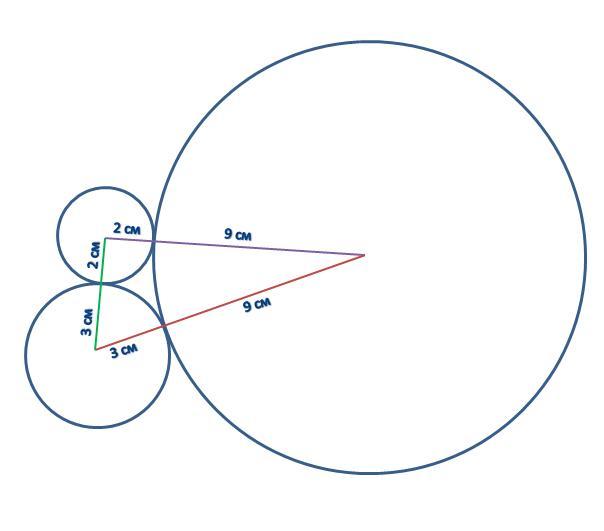
Тут же просто. Даже круги рисовать не нужно, но я нарисовал для наглядности.
Если вершины треугольника находятся в центрах касающихся кругов, значит его стороны образованы радиусами этих кругов.
То есть, 1 сторона Δ = R₁+R₂ = 2+3 = 5;
2 сторона Δ = R₂+R₃ = 3+9 = 12;
3 сторона Δ = R₁+R₃ = 2+9 = 11
Каждый круг строит треугольник двумя своими радиусами.
Поэтому: PΔ = (R₁+R₂) + (R₂+R₃) + (R₁+R₃)
PΔ = (2+3) + (3+9) + (2+9) = 28
или: PΔ = (2+2)+(3+3)+(9+9) = 28
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад