Question

Можете помочь пожалуйста

Answer 1

Ответ:  L=16.

Объяснение:

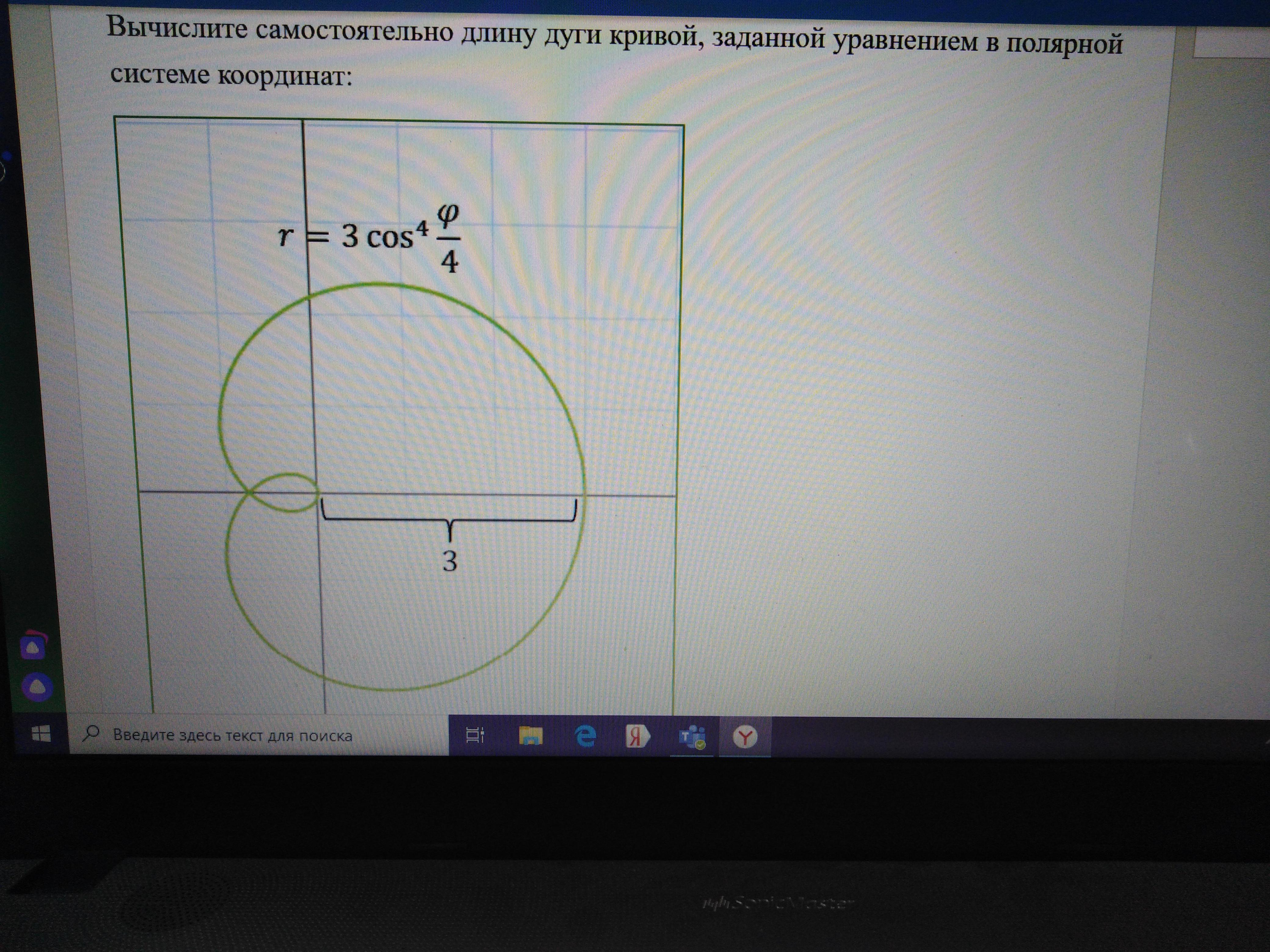
r=3*cos⁴(φ/4)    L=?

Найдём пределы интегрирования, исходя из того,

что радиус должен быть положительным:

соs(φ/4)≥0     ⇒

-π/2+2πn≤φ/4≤π/²+2πn

-2πn+8πn≤φ≤2πn+8πn   ⇒

Интеграл будетиметь интервал -2πn≤φ≤2πn.

Так как кордиоида симметрична оси OX    ⇒

Сдвоенный интервал интеграла равен: 0≤φ≤2π.

L=a*(₀∫²π)√(r²+(r')²)

r'=(cos⁴(φ/4))'=4*cos³(φ/4)*(-sin(φ/4)*(1/4)=cos³(φ/4)*(-sin(φ/4)

(r')²=(cos³(φ/4)*(-sin(φ/4))²=cos³(φ/4)*sin²(φ/4).

√(r²+(r')²=√(cos⁸(φ/4)+cos⁶(φ/4)*sin²(φ/4))=

=√(cos⁶(φ/4)*(cos²(φ/4+sin²(φ/4)=√cos⁶(φ/4)=cos³(φ/4).

L=2*3*(₀∫²π)(cos³(φ/4)=(3/2)*(₀∫²π)(3*cos(φ/4)+cos(3φ/4))=

(3/2)*(3*4*sin(φ/4)+(4/3)*sin(3φ/4)) ₀|²π=

=18*sin(π/2)+2*sin(3π/2)=18+2*(-1)=18-2=16.