Знайдіть висоту трапеції бічні сторони якої становлять 10 см і 17 см, а основи дорівнюють 20 см і 41 см
Ответы
Ответ дал:
0
Ответ:
8 см.
Объяснение:
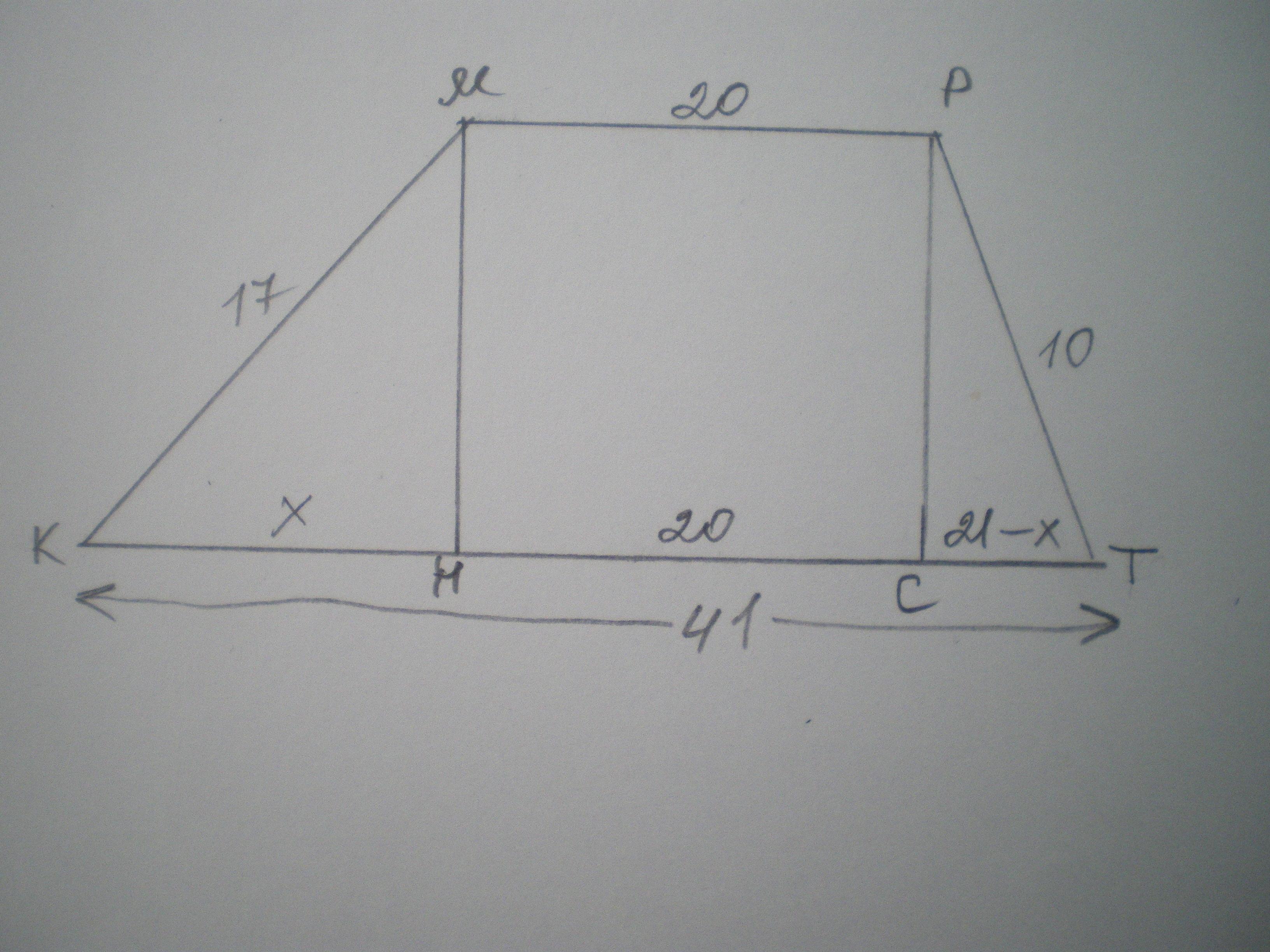
Дано: КМРТ - трапеція, МР=20 см, КТ=41 см, КМ=17 см, РТ=10 см. Знайти висоту МН=РС.
СН=КТ-МР=20 см, тоді КН+СТ=41-20=21 см.
Нехай КН=х, тоді СТ=21-х см.
ΔКМН і ΔРСТ - прямокутні.
За теоремою Піфагора
МН²=КМ²-КН² і РС²=РТ²-СТ², отже КМ²-КН²=РТ²-СТ²
289-х²=100-(21-х)²
289-х²=100-441+42х-х²
42х=630
х=15; КН=15 см
Знайдемо МН за теоремою Піфагора
МН=√(КМ²-КН²)=√(289-225)=√64=8 см
Приложения:
Вас заинтересует
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад