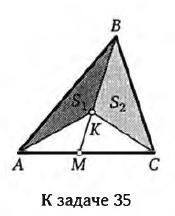
На стороне AC треугольника ABC взяли произвольную точку M. На отрезке BM взяли произвольную точку K. Докажите, что площадь треугольников ABK и CBK относятся как AM:MC
Приложения:
Ответы
Ответ дал:
0
H1, H2 - расстояния от точек A и C до прямой BM.
Площади треугольников с равными высотами относятся как основания.
S(MAK)/S(MCK) =AM/MC
Площади треугольников с равными основаниями относятся как высоты.
S(BAK)/S(BCK) =H1/H2 =S(MAK)/S(MCK) =AM/MC
Вас заинтересует
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад