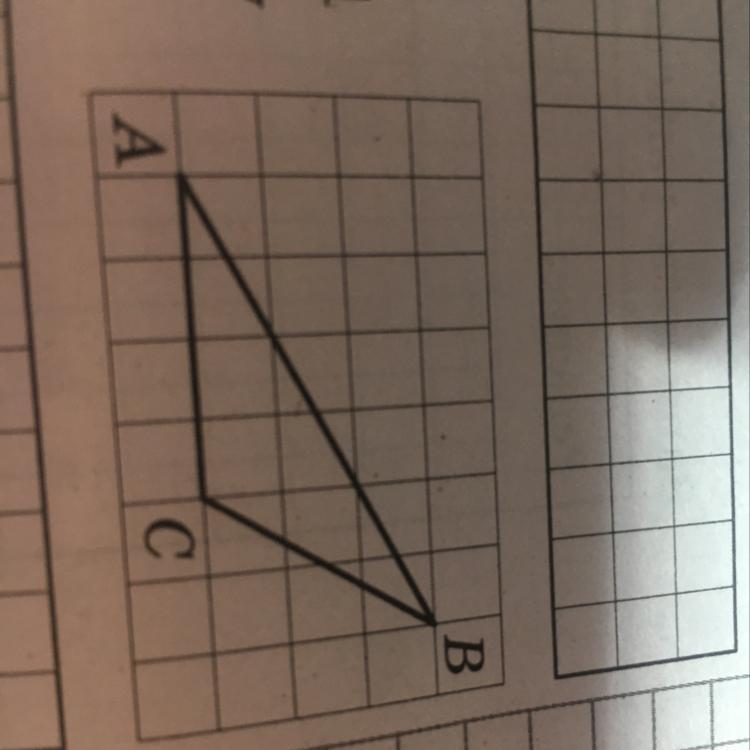
На клетчатой бумаге с размером 1 на 1 изображён треугольник АВС. Найдите длину его медианы, выходящей из точки В.
Приложения:
Ответы
Ответ дал:
0
Ответ:
5 см
Пошаговое объяснение:
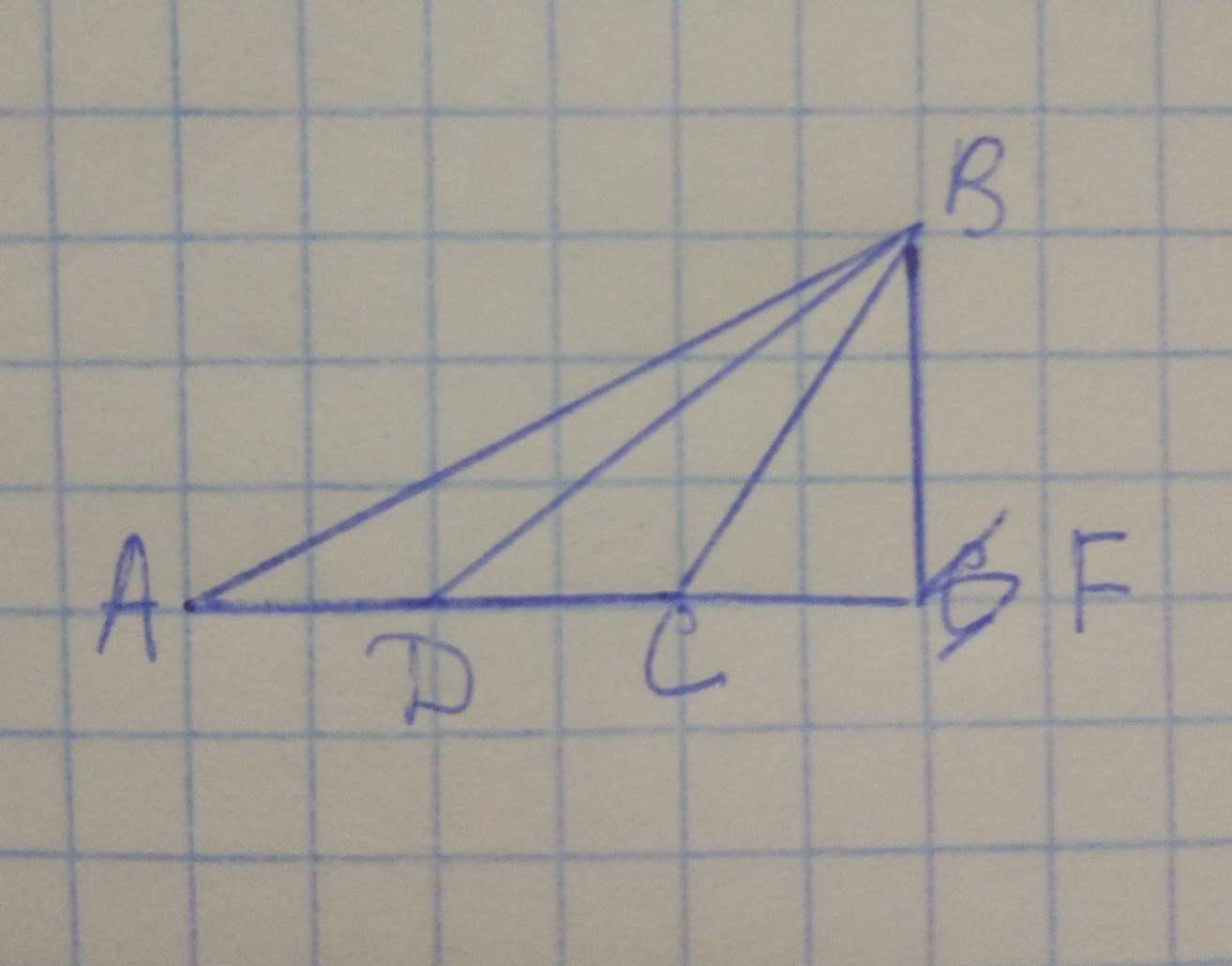
Дано: ∆АВС, AD=CD
Найти BD
Решение
1) По рисунку АС=4 см, поэтому AD=CD=AC/2=4/2=2 см
2) BF перпендикулярно AC. С рисунка видно, что CF=2 см, тогда DF=CD+CF=2+2=4 см
3) ∆BFD, < BFD=90°, с рисунка также видно, что BF=3 см. По теореме Пифагора
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад