Question

Помогите, пожалуйста (40 баллов )
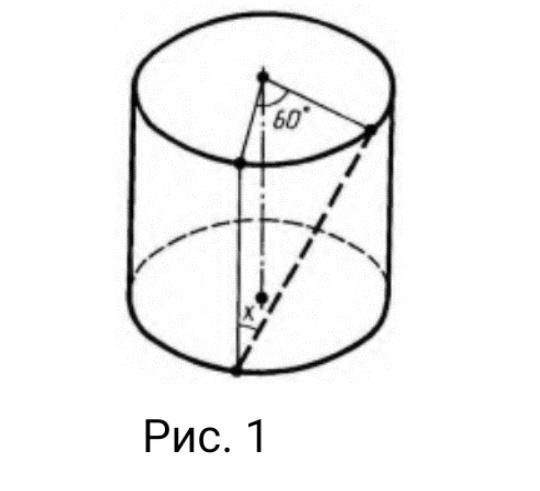
В равностороннем цилиндре (диаметр равен высоте цилиндра) точку окружности верхнего основания сопряжено с точкой окружности нижнего основания. Угол между радиусами, проведенными в эти точки, равна 60 °. Найдите угол x между проведенной прямой и осью цилиндра (рис.1)

Answer 1

Пошаговое объяснение:

ΔОАВ-равнобедренный ОА=ОВ=r, значит ∠А= ∠В=(180°-60°): 2=60°, поэтому он еще и равносторонний. АВ=ОА=r=1/2d , т.к. цилиндр равносторонний и АС=d.

АС⊥(пл.ОАВ)⇒АС⊥АВ⇒ΔАВС-прямоугольный

и в нем катет АВ=1/2d равен половине гипотенузы, значит угол против АВ равен 30°