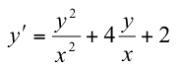Question

Проинтегрировать дифференциальное уравнение.

Answer 1

Это линейное однородное дифференциальное уравнение первого порядка. Для этого уравнения всегда осуществляется замена $y=ux$, тогда $y'=u'x+u$, получаем :

$u'x+u=u^2+4u+2\ \ u'x=u^2+3u+2$

Получили дифференциальное уравнение с разделяющимися переменными.

$displaystyle int dfrac{du}{u^2+3u+2}=int dfrac{dx}{x}~~~Rightarrow~~~int dfrac{du}{(u+1)(u+2)}=int dfrac{dx}{x}\ \ \ int dfrac{(u+2)-(u+1)}{(u+1)(u+2)}du=int dfrac{dx}{x}~~Rightarrow~~ int left(dfrac{1}{u+1}-dfrac{1}{u+2}right)du=int dfrac{dx}{x}\ \ \ ln |u+1|-ln |u+2|=ln |x|+ln C\ \ ln Bigg|dfrac{u+1}{u+2}Bigg|=ln Big|CxBig|\ \ \ dfrac{u+1}{u+2}=Cx~~~Rightarrow~~~ 1+dfrac{1}{u+2}=Cx~~~Rightarrow~~~dfrac{1}{u+2}=Cx-1$

$u+2=dfrac{1}{Cx-1}\ \ u=dfrac{1}{Cx-1}-2$

Выполним обратную замену

$dfrac{y}{x}=dfrac{1}{Cx-1}-2~~~Rightarrow~~~ boxed{y=dfrac{x}{Cx-1}-2x}$

Получили общее решение диф. уравнения.

Answer 2

Ответ:

$x=frac{C(y+x)}{y+2x}$

Пошаговое объяснение:

$frac{y}{x} =t\y=tx\y'=t'x+t$

$t'x+t=t^2+4t+2\\ t'x=t^2+3t+2\\t'=frac{t^2+3t+2}{x} \\frac{dt}{dx} =frac{t^2+3t+2}{x}\\frac{dx}{x} =frac{dt}{t^2+3t+2}\\lnx=-ln|t+2|+ln|t+1|+lnC\\lnx=ln{frac{C(t+1)}{t+2} }\\x=frac{C(t+1)}{t+2}\\x=frac{C(frac{y}{x} +1)}{frac{y}{x}+2}=frac{C(y+x)}{y+2x}$