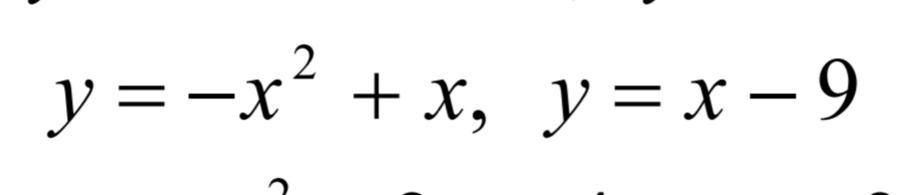Question

Обчислити площу фігури(інтеграли)
35 балів

Answer 1

$y = - {x}^{2} + x, : y = x - 9$

Щоб знайти межі інтегрування, знайдемо точки, де дані дві функції перетинаються:

$- {x}^{2} + x = x - 9 \ - {x}^{2} = - 9 \ {x}^{2} = 9 \ x = ±3$

Знаходимо площу:

$int_{ - 3}^{3} ( - {x}^{2} + x - x + 9)dx = int_{ - 3}^{3} 9 - {x}^{2} dx = \ = 9x - frac{ {x}^{3} }{3} |_{ - 3}^{3} = 27 - frac{27}{3} -( - 27) + frac{ - 27}{3} = 36$

Відповідь: 36 кв. од.