Question

40 БАЛОВ!!!
Дві площини перетинаються під кутом 60º. Точка А, яка лежить в одній з цих площин, віддалена від другої площини на відстань 4$sqrt{3}$ см. Знайти відстань від точки А до лінії перетину площин.

Answer 1

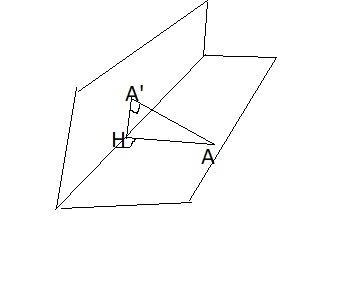
Відстань від точки A до другої площини — це довжина перпендикуляра AA', опущеного з точки A на іншу площину. Відстань від т. A до лінії перетину площин — це величина перпендикуляра AH, опущеного з т. A на пряму перетину.

З'єднавши точки A' та H, отримаємо прямокутний трикутник AA'H (тому що AA' перпендикулярний до будь-якої прямої іншої площини). За теоремою про 3 перпендикуляри A'H буде перпендикулярний і прямій перетину, а, отже, є проекцією AH на другу площину, і в такому випадку кут AHA' і буде кутом між двома площинами.

З прямокутного ΔAHA' знайдемо АН:

$sinalpha = frac{AA'}{AH} :: Rightarrow :: AH = frac{AA'}{sinalpha } \AH = frac{4sqrt{3}}{frac{sqrt{3} }{2} } = frac{4sqrt{3}cdot 2}{sqrt{3}} = 8 :: (cm)$

Відповідь: Відстань від точки А до лінії перетину площин рівна 8 см.