Question

помогите пожалуйста задание в файле буду благодарен

Answer 1

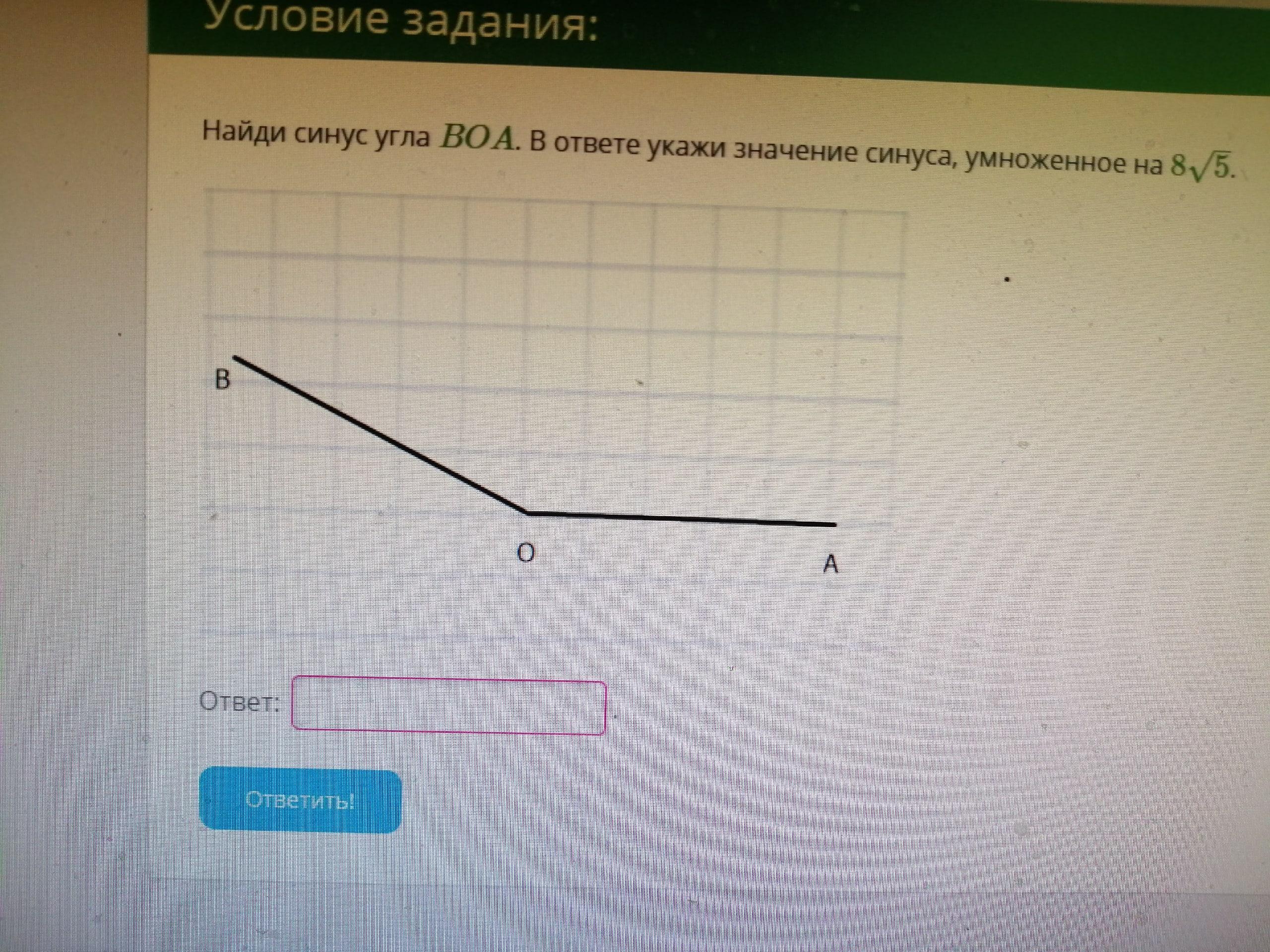
Продлим отрезок OA и проведём отрезок BK, перпендикулярный к OA.

Получим: BK = 2, KO = 4.

Тогда исходя из того, что ∆ВКО – прямоугольный найдём угол ВОК:

$tg(ВОК) = frac{ВК}{ОК} \ tg(ВОК) = frac{2}{4} = frac{1}{2} \ ВОК = arctg( frac{1}{2} )$

Значит смежный угол ВОА = π - arctg(1/2), а синус угла ВОА:

$sin(ВОА) = sin(pi - arctg( frac{1}{2} )) = sin( arctg( frac{1}{2} ) )$

Вычислим величину синуса этого угла за формулой:

$sin( arctg(a)) = frac{a}{ sqrt{1 + {a}^{2} }}$

Получим:

$sin( arctg( frac{1}{2} ) ) = frac{ frac{1}{2} }{ sqrt{1 + frac{1}{4} } } = frac{ sqrt{5} }{5}$

За условием ответ умножаем на 8√5:

$frac{ sqrt{5} }{5} times 8 sqrt{5} = frac{ {( sqrt{5}) }^{2} }{5} times 8 = 8$

Ответ: 8.