Question

Условие и вопрос на рисунке!!!

Answer 1

Ответ:

Доказательство в объяснении.

Объяснение:

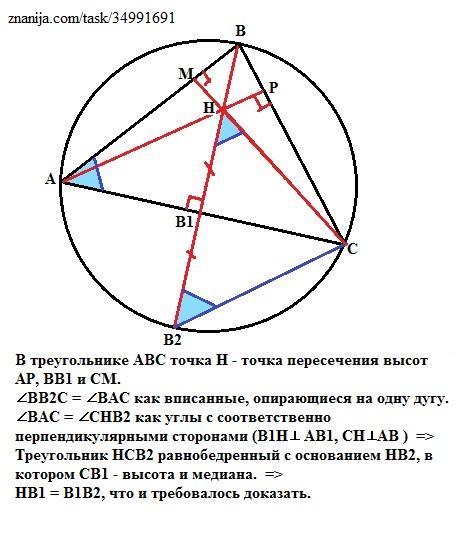
Около треугольника АВС описана окружность. Продолжение высоты ВВ1 пересекает окружность в точке В2. Точка Н - точка пересечения высот треугольника. Доказать, что НВ1 = В1В2.

Решение:

Проведем высоты треугольника.

В треугольнике АВС точка Н - точка пересечения высот АР, ВВ1 и СМ.

∠ВВ2С = ∠ВАС как вписанные, опирающиеся на одну дугу ВС.

∠ВАС = ∠СНВ2 как углы с соответственно перпендикулярными сторонами

(В1Н⊥ АВ1, СН⊥АВ ) =>

Треугольник НСВ2 равнобедренный с основанием НВ2, в котором СВ1 - высота и медиана. =>

НВ1 = В1В2, что и требовалось доказать.