Question

ПОМОГИТЕ, ПОЖАЛУЙСТА!


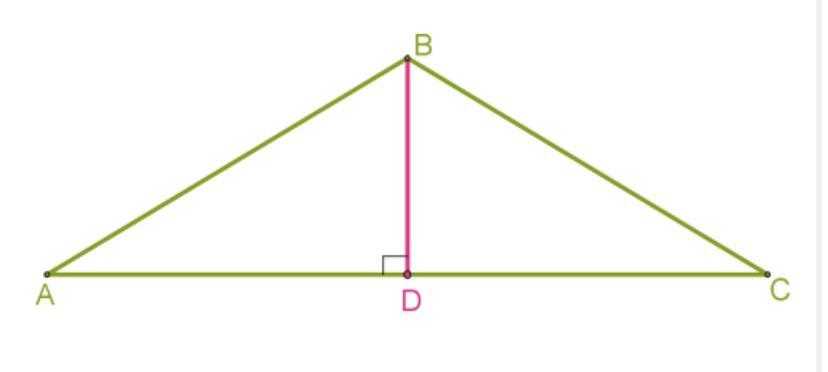
В равнобедренном треугольнике ABC проведена высота BD к основанию AC.
Длина высоты — 6,3 см, длина боковой стороны — 12,6 см.
Определи углы этого треугольника.

∡ BAC = °

∡ BCA = °

∡ ABC = °

Answer 1

Ответ:

BAC=BCA=30°, ABC=120°

Объяснение:

Если длинна высоты(что в даном случае катет) равна 6.3 см, при етом длина боковой стороны(гипотенузе) 12.6 см, а ети числа относяться как 1/2, то угол, который лежит против етого катета = 30°. ( за свойством катета и гепотинузы, что относяться 1/2) .

то есть, угол BAC = BCA (как угли у подножия равнобедреного триугольника) = 30°.

за основным свойством про сумму углов триугольника имеем:

угол ABC = 180°- 30°*2=120°