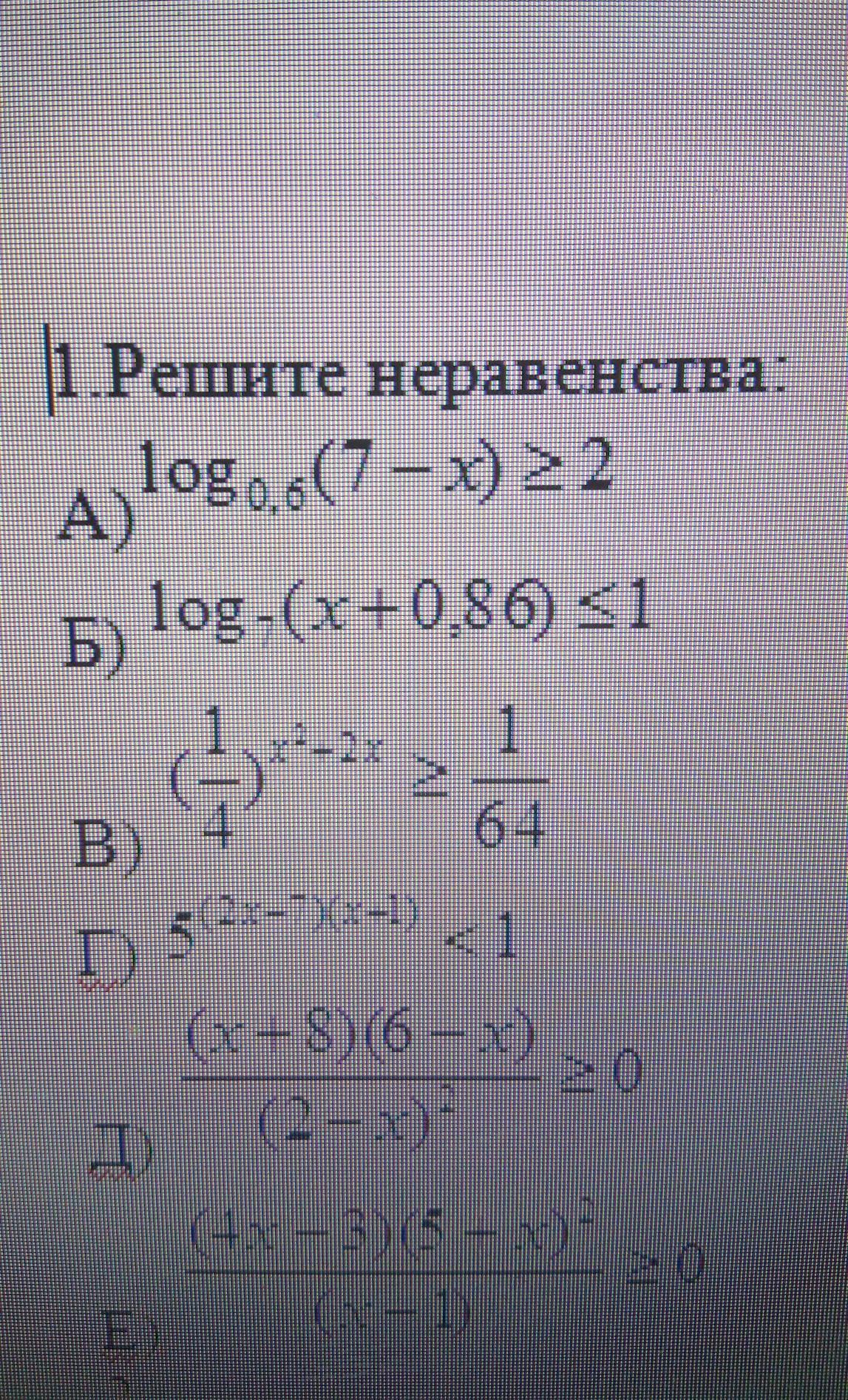Ответы
Ответ дал:
0
Ответ:
Объяснение:
Ответ: x∈[6,64;7).
Б)
Ответ: х∈(-0,86;6,14]
B)
Г)
-∞__+__-1__-__3,5__+__+∞
x∈(-1;3,5).
Д)
-∞_-_(2)_-_6__+__8__-__+∞
x∈[6;8].
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
9 лет назад