Question

З точки, що знаходиться на відстані 12 см від площини, проведено дві похилі довжиною 13см. і 20 см. Відстань між основами похилих становить 19 см. Обчислити кут між проекціями цих похилих.

Answer 1

Задача: Из точки, находящейся на расстоянии 12 см от плоскости, проведены две наклонные длиной 13 см и 20 см. Расстояние между основаниями наклонных составляет 19 см. Вычислить угол между проекциями этих наклонных.

Решение:

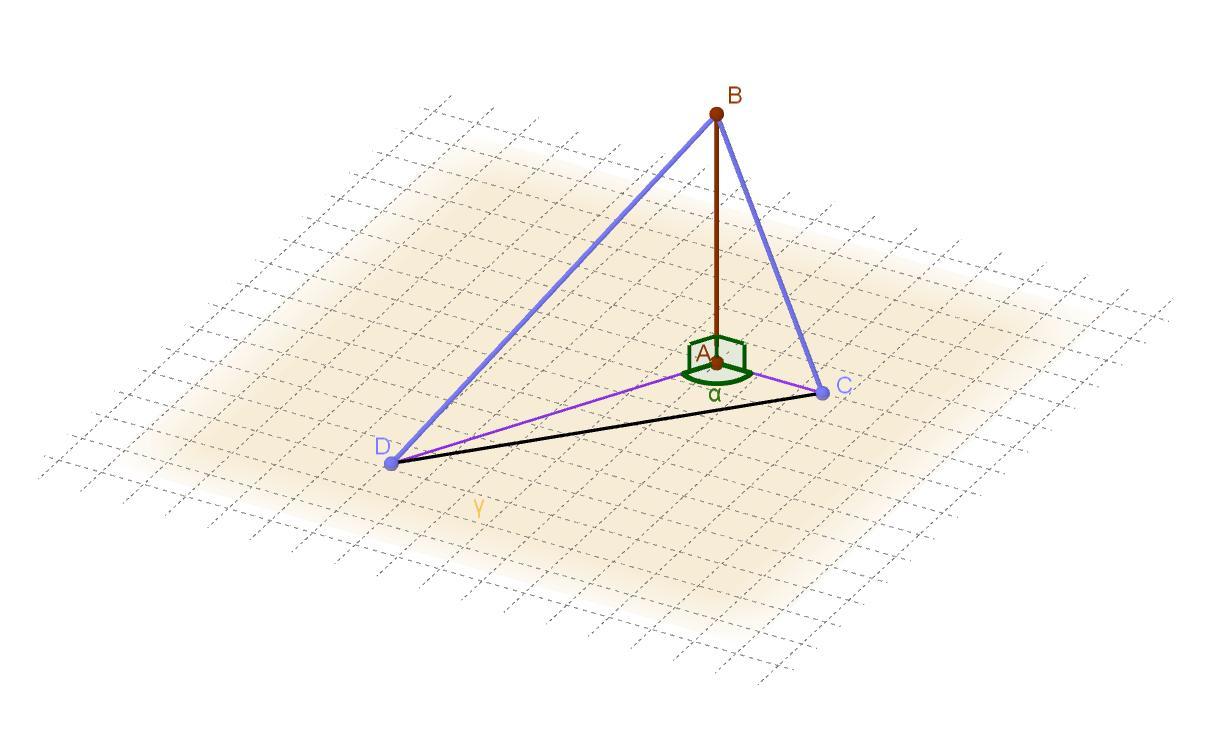
Обозначим плоскость как γ, перпендикуляр из точки к плоскости как AB, наклонные как BD и DC, тогда AD и AC — проекции наклонных, отрезок CD — расстояние между основами наклонных, угол α — угол между проекциями наклонных.

ΔBDA и ΔBCA — прямые, т.к перпендикулярны к плоскости (AB⊥γ).

Вычислим AD за т. Пифагора:

    $AD^2=BD^2-AB^2 :: rightarrow :: AD= sqrt{BD^2-AB^2} \AD= sqrt{20^2-12^2} = sqrt{400-144} = sqrt{256} = 16 :: (cm)$

Вычислим AC за т. Пифагора:

    $AC = sqrt{BC^2-AB^2} \AC = sqrt{13^2-12^2} = sqrt{169-144}=sqrt{25} =5 :: (cm)$

Воспользуемся теоремой косинусов для нахождения угла (α) тр-ка по 3-м сторонам:    

    $cosalpha = frac{AD^2+AC^2-CD^2}{2cdot ADcdot AC} \cosalpha = frac{16^2+5^2-19^2}{2cdot 16cdot 5} = frac{256+25-361}{160} = frac{-80}{160} =-frac{1}{2} \cos(-frac{1}{2} ) = 120°\alpha = 120°$

Ответ: Угол между проекциями наклонных равен 120°.