Question

Задание на фотократочке, за решение буду сердечно благодарен!

Answer 1

Задача: Квадрат и прямоугольник, площади которых соответственно равны 64 и 120 см², имеют общую сторону. Угол между площадями фигур составляет 60°. Вычислить расстояние между сторонами квадрата и прямоугольника, противоположными к их общей стороне.

Решение:

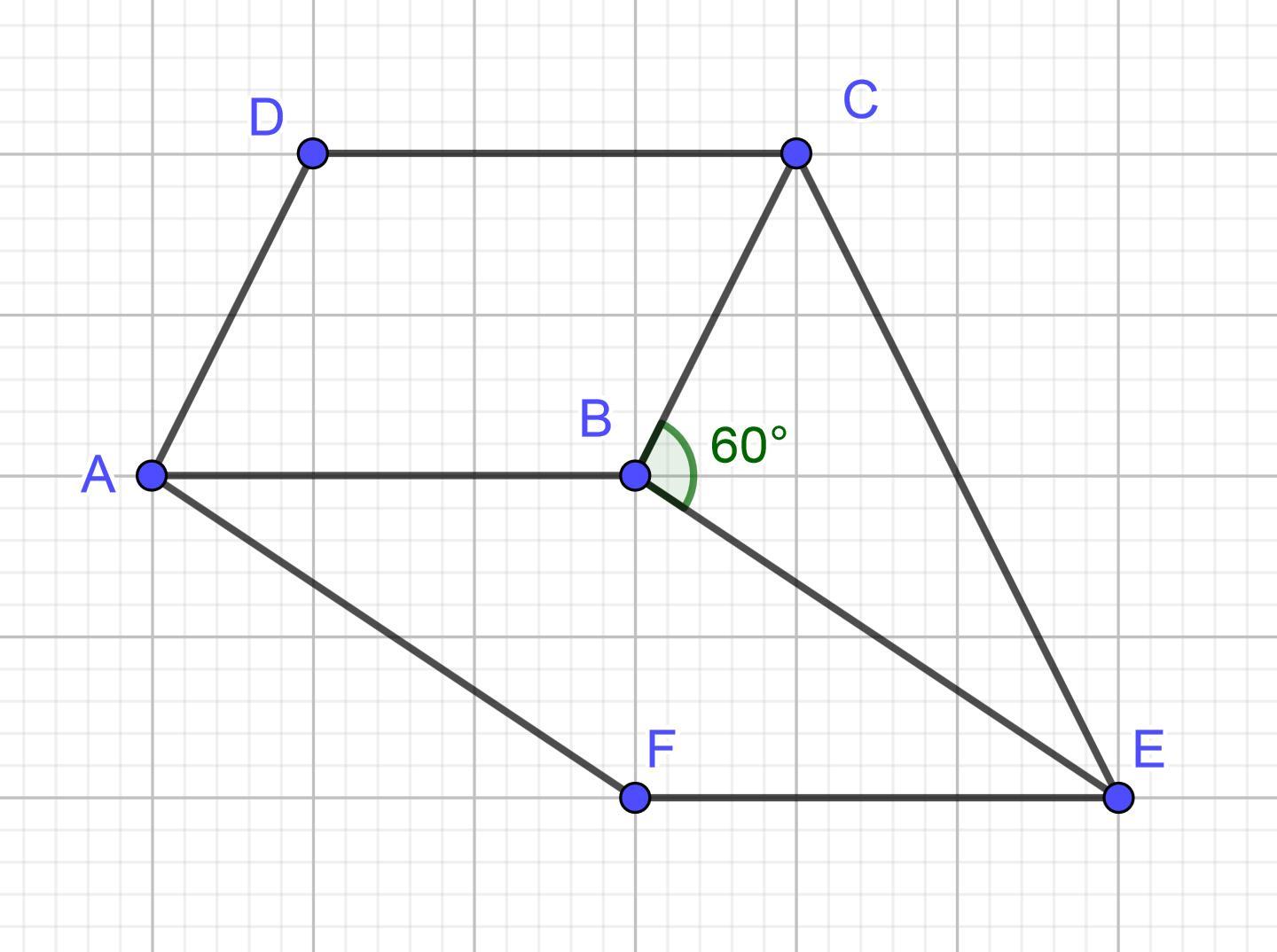
Пусть даны квадрат ABCD и прямоугольник ABEF, AB — общая сторона, ∠СВЕ = 60°.

Зная площадь квадрата, найдем длину его стороны:

    $S = a^2 :: Rightarrow :: a =sqrt{S}\a = sqrt{64} = 8$

    $a = CB = 8 (cm)$

Зная площадь и сторону прямоугольника, найдем его вторую сторону:

    $S = acdot b :: Rightarrow :: b =S:a\b = 120:8 = 15$

    $b = BE = 15 (cm)$

Расстояние от т. С до т. Е — и есть расстояние между сторонами квадрата и прямоугольника.

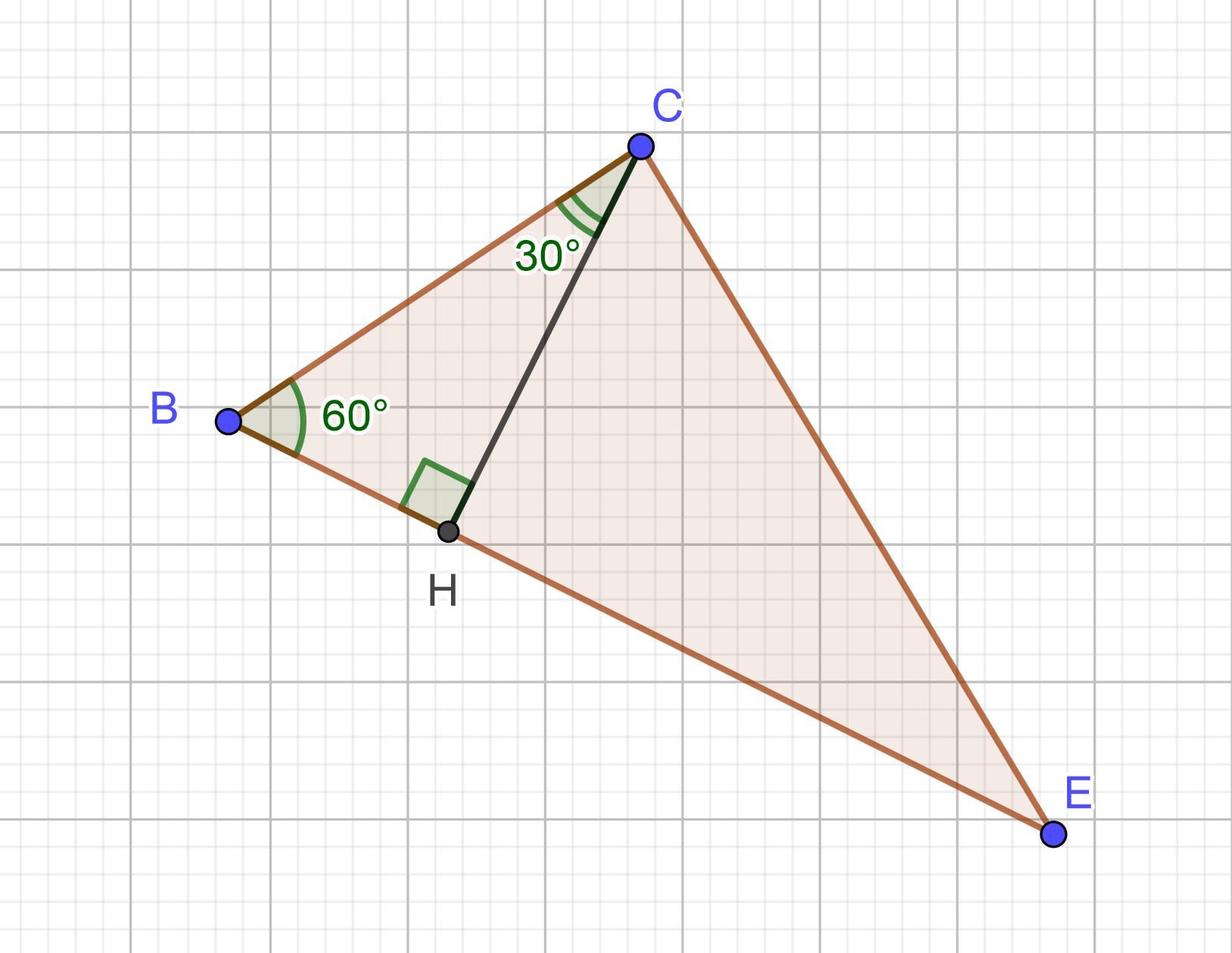
Р-м ΔCEB:

BC = 8 см, BE = 15 см, ∠CBE = 60°

Проведем высоту CH на сторону BE  ⇒  получим для прямоугольных треугольника.

    $angle BCH = 180-90-60 = 30°$

    $BH = BC:2 = 8:2 = 4 :: (cm)$ — по свойству катета, лежащего напротив угла 30°.

Найдем длину отрезка CH по т. Пифагора:

    $CH^2 = BC^2-BH^2 :: Rightarrow :: CH = sqrt{BC^2-BH^2} \CH = sqrt{8^2-4^2} = sqrt{64-16}=sqrt{48} :: (cm)$

Найдем длину отрезка EH:

    $EH = BE-BH = 15-4 = 11 :: (cm)$

Найдем длину отрезка CE по т. Пифагора:

    $CE=sqrt{CH^2+EH^2} \CE=sqrt{(sqrt{48}) ^2+11^2} = sqrt{48+121} =sqrt{169} = 13 :: (cm)$

Ответ: Расстояние между сторонами квадрата и прямоугольника равно 13 см.