Question

Помогите.задание на фото

Answer 1

Ответ:

Объяснение:

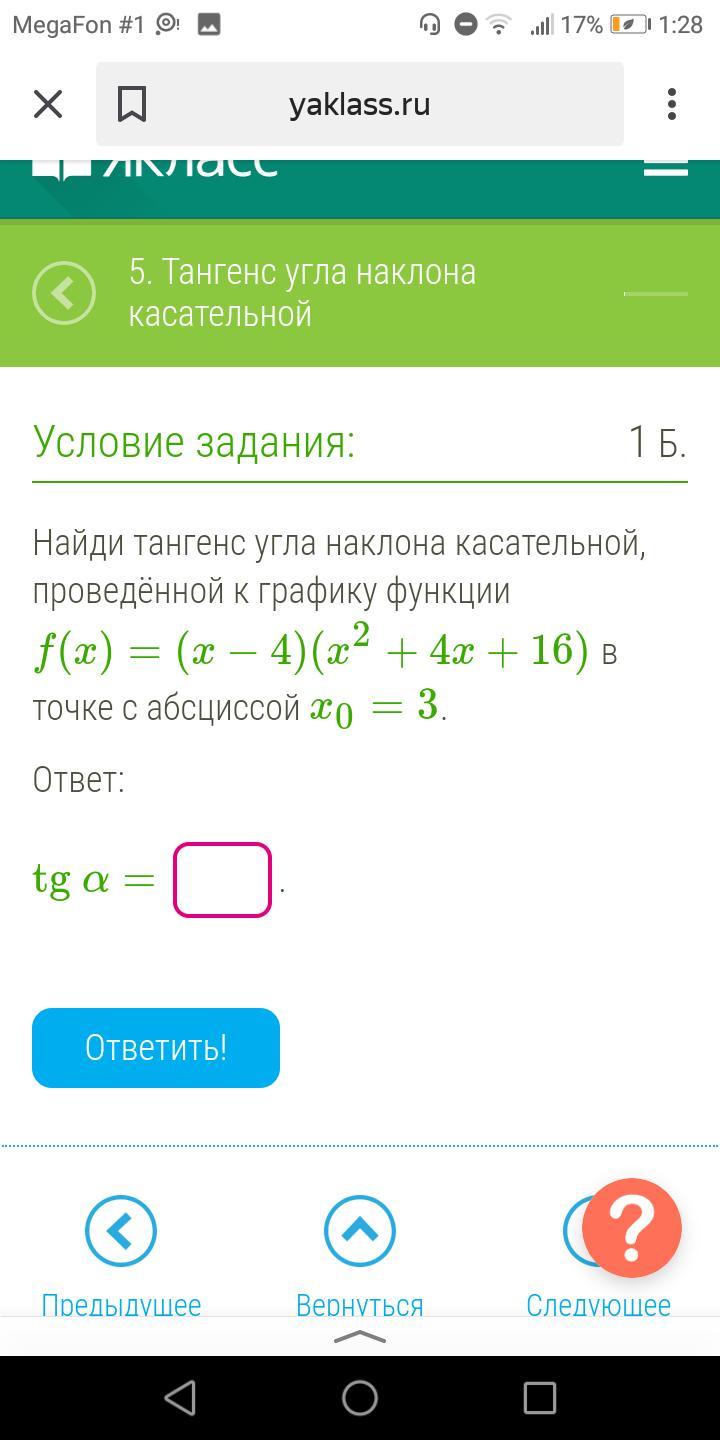
Тангенс угла наклона касательной, проведенной к графику функции f(x) в точке x0 равен значению производной f'(x) в точке x=x0:

$tga=f'(x_0);\f'(x)=((x-4)(x^2+4x+16))'=(x-4)'(x^2+4x+16)+(x^2+4x+16)'(x-4)=\=x^2+4x+16+(2x+4)(x-4)=x^2+4x+16+2x^2-8x+4x-16=3x^2;\f'(x_0)=f'(3)=3*3^2=3*9=18$