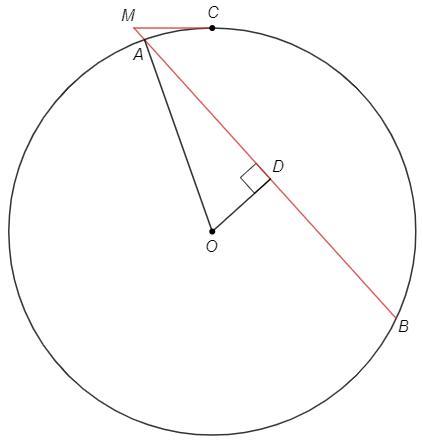
Дана окружность (O;OC). Из точки M, которая находится вне окружности, проведена секущая MB и касательная MC.
OD — перпендикуляр, проведённый из центра окружности к секущей MB и равный 5 см.
Найди радиус окружности, если известно, что MB равен 25 см и MC равен 5 см.
Ответы
Ответ дал:
0
В сантиметрах.
MA - внешняя часть секущей.
Теорема о касательной и секущей
MC^2 =MA*MB => 25=MA*25 => MA=1
Радиус, перпендикулярный хорде, делит ее пополам.
AD =AB/2 =(MB-MA)/2 =12
По теореме Пифагора
OA =√(OD^2 +AD^2) =13 (см)
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
10 лет назад