Question

Изобразите на комплексной плоскости множество точек z, удовлетворяющих условию 2 < |z| < 3

Answer 1

$2 < |z| < 3$

Распишем модуль:

$2 < sqrt{x^2+y^2} < 3$

$2^2 <x^2+y^2 < 3^2$

Уравнения $x^2+y^2=2^2$ и $x^2+y^2=3^2$ - уравнения окружности.

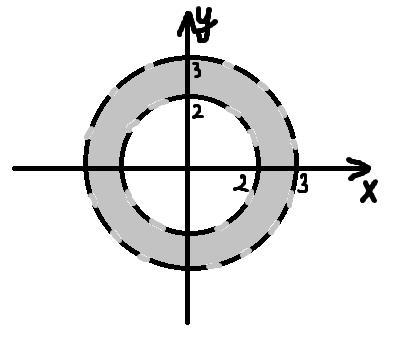
Неравенство $x^2+y^2 >2^2$ определяет часть плоскости вне окружности с радиусом 2.

Неравенство $x^2+y^2 <3^2$ определяет часть плоскости внутри окружности с радиусом 3.

Значит, неравенство $2^2 <x^2+y^2 < 3^2$ определяет кольцо, ограниченное окружностями с радиусами 2 и 3.