Ответы
Ответ дал:
0
Ответ:
Объяснение:
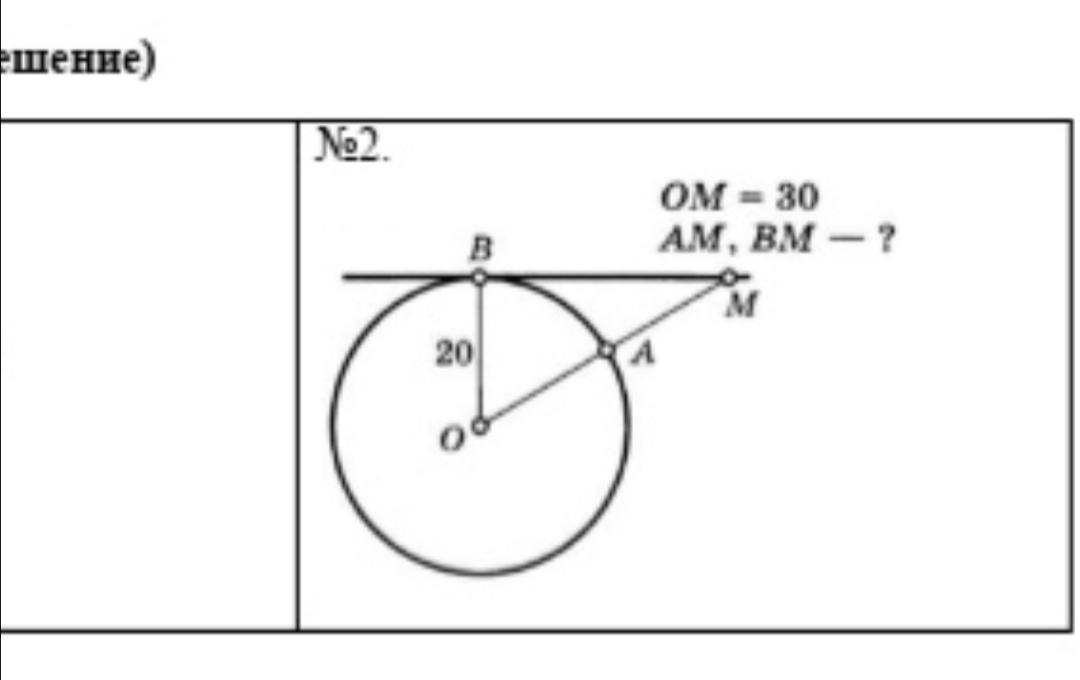
Рассмотрим треугольник OMB: он прямоугольный так как касательная и радиус в точке пересечения образуют 90 градусов угол
По теореме Пифагора находим BM:
=
-
=900-400=500
BM=10*
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: =OM*AM
AM=/OM
AM=500/30=16,6
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад