В прямоугольном треугольнике с острым углом в 30° больший катет равен равен 18 см. На какие отрезки делит этот катет биссектриса большего острого угла треугольника?
Можно написать просто ответ без объяснений
Andr1806:
По правилам сервиса НЕЛЬЗЯ написать просто ответ без объяснений. Такой ответ будет удален.
какой именно ответ ?
Не полный, то есть только ответ без объяснений или решение не всех задач.
а ответ к какой задаче вас не устроил ?
Не устроил условие Вашего задания: "Можно написать просто ответ без объяснений". Если кто-то ответит так, то его ответ будет удален.
хорошо я поняла
прошу прощение
Ответы
Ответ дал:
1
Ответ:
АМ = 6 см, МВ = 12 см.
Объяснение:
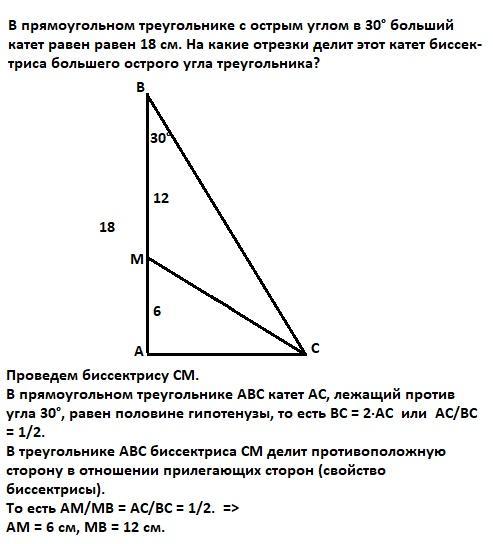
Проведем биссектрису СМ.
В прямоугольном треугольнике АВС катет АС, лежащий против угла 30°, равен половине гипотенузы, то есть ВС = 2·АС или АС/ВС = 1/2.
В треугольнике АВС биссектриса СМ делит противоположную сторону в отношении прилегающих сторон (свойство биссектрисы).
То есть АМ/МВ = АС/ВС = 1/2. =>
АМ = 6 см, МВ = 12 см.
Приложения:
как сменить никнейм ?
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад