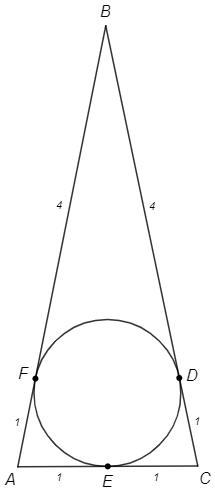
В равнобедренном треугольнике ABC с основанием AC, точка касания вписанной окружности делит сторону BC на отрезки длиной 4 и 1, считая от вершины B. Найдите периметр треугольника.
помогите пожалуйста
siestarjoki:
Стороны являются касательными. Отрезки касательных из одной точки равны.
P=12
нерпавельно
Ответы
Ответ дал:
0
Отрезки касательных, проведенных из одной точки, равны.
AE=AF, BF=BD, CD=CE
AB=BC (ABC - равнобедренный), BF=BD => AF=CD
AF=AE=CD=CE =1
AB=BC =4+1 =5
P= AB+BC+AC =5+5+2 =12 (см)
Приложения:
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад