Question

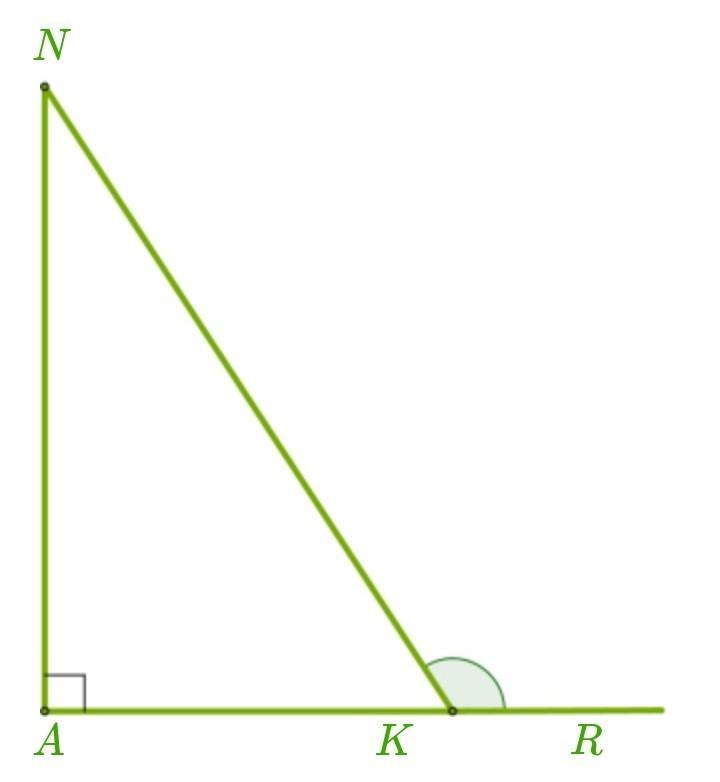
Дан прямоугольный треугольник ANK и внешний угол угла ∡ K.

Определи величины острых углов данного треугольника, если ∡ NKR = 114°.

 

∡ K = °;

 

∡ N = °.

​

Answer 1

Ответ:

Т.к. углы NKA и NKR - смежные, то они в сумме должны быть 180 градусов. Следовательно угол NKA(угол К)=180-114=66.

Т.к. угол А=90, можно найти угол N: 180-(90+66)=24.

Объяснение:

Answer 2

Объяснение:

<NKR И <NKA - смежные углы. (В сумме смежные углы дают 180°)

Значит чтобы найти <NKA нужно от 180° отнять <NKR:

<NKA =180°-114°=66°(<К)

В сумме все углы треугольника дают 180°.

Значит чтобы найти ANK мы должны от 180° отнять <К и отнять <А(угол А 90°):

180°-66°-90°=24°.

Ответ:<К=66°; <N=24°