Question

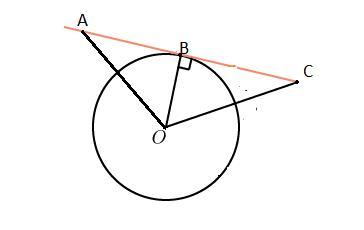
Прямая касается окружности с центром O в точке B. На касательной по разные стороны от точки B отложены равные отрезки BA и BC. Доказать,что OA = OB.

Answer 1

Дано :Окр. О(r)ВС-касательная , А∈ВС, ВА=ВС.

Доказать :OA = OС

Объяснение:

Касательная , проведенная в точку касания, перпендикулярна радиусу ⇒∠АВО=∠СВО=90°

ΔАВО=ΔСВО как прямоугольные по двум катетам : АВ=СВ по условию, ВО-общая. В равных треугольниках соответственные элементы равны , значит ОА=ОС.

Answer 2

Но смотрите,тут нужно показать что AO = OB,а по вашему объявлению AO = CO,не верно если так подумать

Answer 3

Тогда мое решение не соответствует поставленному вопросу. Ставьте -нарушение.

Answer 4

Может, кто-то еще попробует.....

Answer 5

Ток в условии AC касательная.