Question

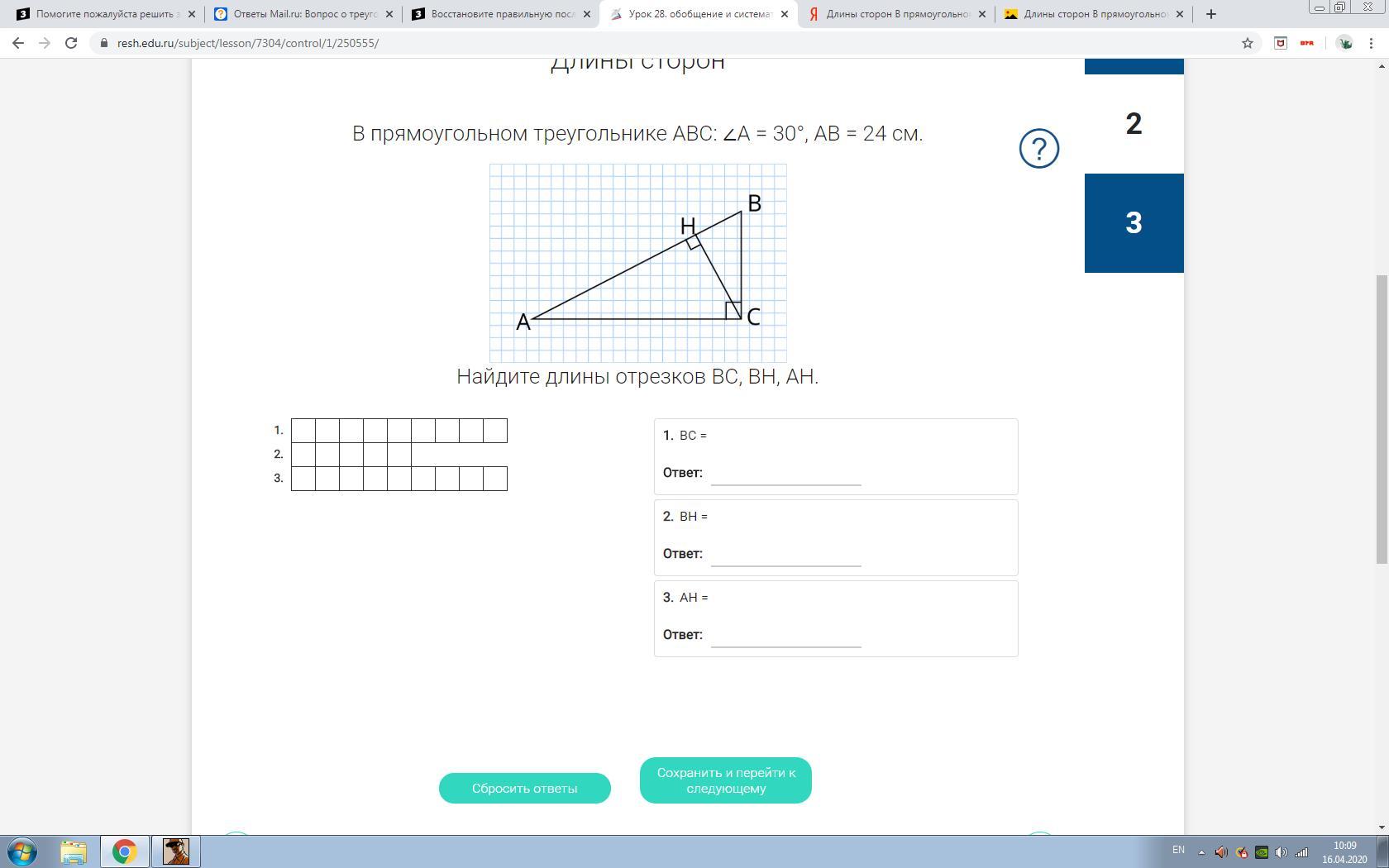
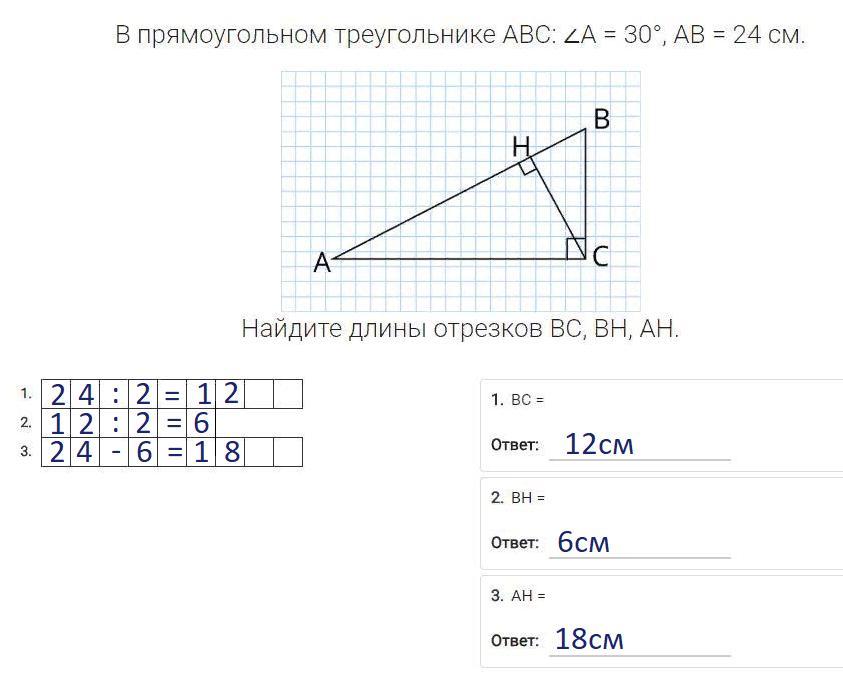
В прямоугольном треугольнике ABC: ∠A = 30°, AB = 24 см.
Найдите длины отрезков BC, BH, AH.

Answer 1

• Катет лежащий против угла в 30° равен половине гипотенузы.

В △ABC:

∠A = 30°;  BC - катет, лежащий напротив ∠А;

⇒ BC = AB:2 = 24см:2 = 12см.

По рисунку CH⊥AB  ⇒  ∠AHC = 90°.

• Сумма острых углов прямоугольного треугольника равна 90°.

△AHC - прямоугольный т.к. ∠AHC = 90°  ⇒

⇒ ∠A+∠C = 90°;  ∠C = 90°-∠A = 90°-30° = 60°.

∠ACB = ∠ACH+∠BCH т.к. они его составляют;

∠BCH = ∠ACB-∠ACH;

∠BCH = 90°-60° = 30°.

△CHB - прямоугольный т.к. ∠H = 90°,

∠C = 30°; HB - катет, лежащий напротив ∠C;

⇒ HB = BC:2 = 12см:2 = 6см.

AB = AH+HB т.к. они его составляют;

AH = AB-HB;

AH = 24см-6см = 18см.

Ответ: BC = 12см; BH = 6см; AH = 18см.