Из точки, отстоящей от плоскости на расстоянии 10 м, проведены две наклонные, образующие с плоскостью углы 45°, а между собой 30°. Найдите расстояние между концами наклонных.
Ответы
Ответ дал:
0
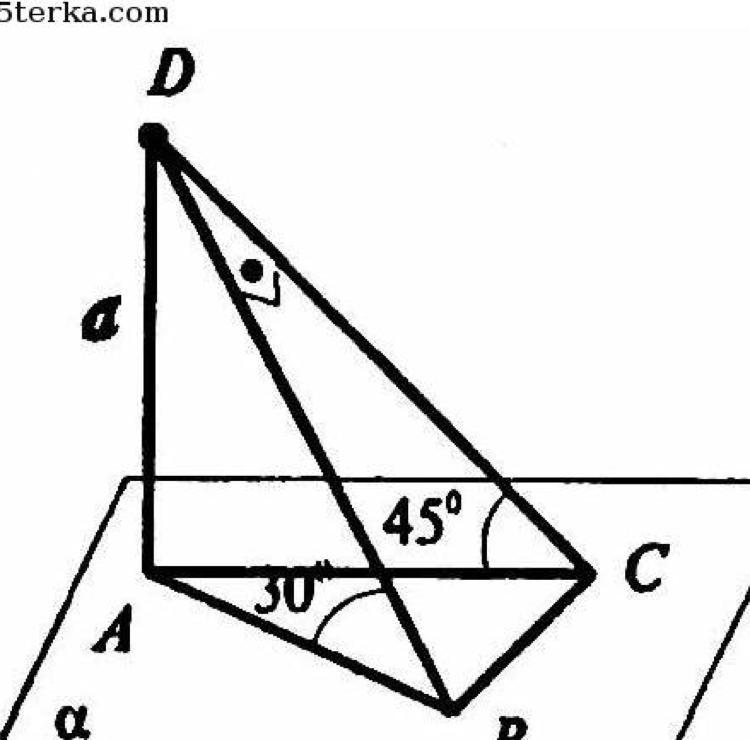
Пусть DC и DB данные наклонные.
Проведем AD — перпендикуляр к плоскости α. АВ и АС — проекции наклонных DB и DC на плоскость α. Треугольники DAB и DAC — прямоугольные. Так что DC = а : sin45° = a√2 ; DB = а : sin30° = 2a.
Далее, ΔBDC — прямоугольный (по условию). Тогда по теореме Пифагора:
BC= √DB^2+DC^2= √2a^2+4a^2=a √6
Проведем AD — перпендикуляр к плоскости α. АВ и АС — проекции наклонных DB и DC на плоскость α. Треугольники DAB и DAC — прямоугольные. Так что DC = а : sin45° = a√2 ; DB = а : sin30° = 2a.
Далее, ΔBDC — прямоугольный (по условию). Тогда по теореме Пифагора:
BC= √DB^2+DC^2= √2a^2+4a^2=a √6
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад