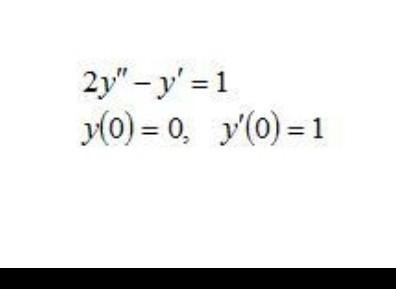Question

2y"-y'=1 y(0)=0. y'(0)=1 помогите ​

Answer 1

$2y'' - y' = 1, y(0)=0, y'(0)=1$

Имеем задачу Коши. Решим ее.

$2y'' - y' = 1$

Данное уравнение допускает понижение его порядка, поэтому сделаем соответствующую подстановку:

$y' = p; y'' = p'$, где $p = p(x)$

Имеем:

$2p' - p = 1$

$p' - dfrac{1}{2} p = dfrac{1}{2}$ — неоднородное линейное дифференциальное уравнение первого порядка

Воспользуемся методом Бернулли: $p = uv; p' = u'v + uv'$, где $u = u(x), v = v(x)$

Следовательно, $u'v + uv' - dfrac{1}{2}uv = dfrac{1}{2}$

$u'v + uleft(v' - dfrac{1}{2}vright) = dfrac{1}{2}$

Пусть $v' - dfrac{1}{2}v = 0$. Тогда $u'v = dfrac{1}{2}$

Имеем: $displaystyle left { {{v' - dfrac{1}{2}v = 0} atop {u'v = dfrac{1}{2} }} right.$

Решим первое дифференциальное уравнение:

$v' - dfrac{1}{2}v = 0$

$dfrac{dv}{dx} = dfrac{1}{2}v$

$dfrac{dv}{v} = dfrac{1}{2} dx$

$displaystyle intdfrac{dv}{v} = intdfrac{1}{2} dx$

$ln |v| = dfrac{1}{2}x$

$v = e^{0,5x}$

Решим второе дифференциальное уравнение, подставляя $v = e^{0,5x}$:

$u'e^{0,5x} = dfrac{1}{2}$

$dfrac{du}{dx} = dfrac{1}{2e^{0,5x}}$

$du = dfrac{dx}{2e^{0,5x}}$

$displaystyle int du = int dfrac{dx}{2e^{0,5x}}$

$u = -dfrac{1}{e^{0,5x}}+C_{1}$

Таким образом, $p = uv = left(-dfrac{1}{e^{0,5x}}+C_{1}right)e^{0,5x} = -1 +C_{1}e^{0,5x}$

Сделаем обратную подстановку:

$y' = -1 +C_{1}e^{0,5x}$

$displaystyle y = int (-1 +C_{1}e^{0,5x})dx = -x + 2C_{1}e^{0,5x} + C_{2}$

Из начальных условий $y(0)=0, y'(0)=1$ имеем:

$displaystyle left { {{0 = 2C_{1} + C_{2}} atop {1 = -1 + C_{1} }} right.$

$displaystyle left { {{C_{1} = 2 } atop {C_{2} = -2C_{1} = -4}} right.$

Частное решение:

$displaystyle y = -x + 4e^{0,5x} -4$

Ответ: $displaystyle y = -x + 4e^{0,5x} -4$

Answer 2

Да, согласен. Способов решений для этого уравнения много.