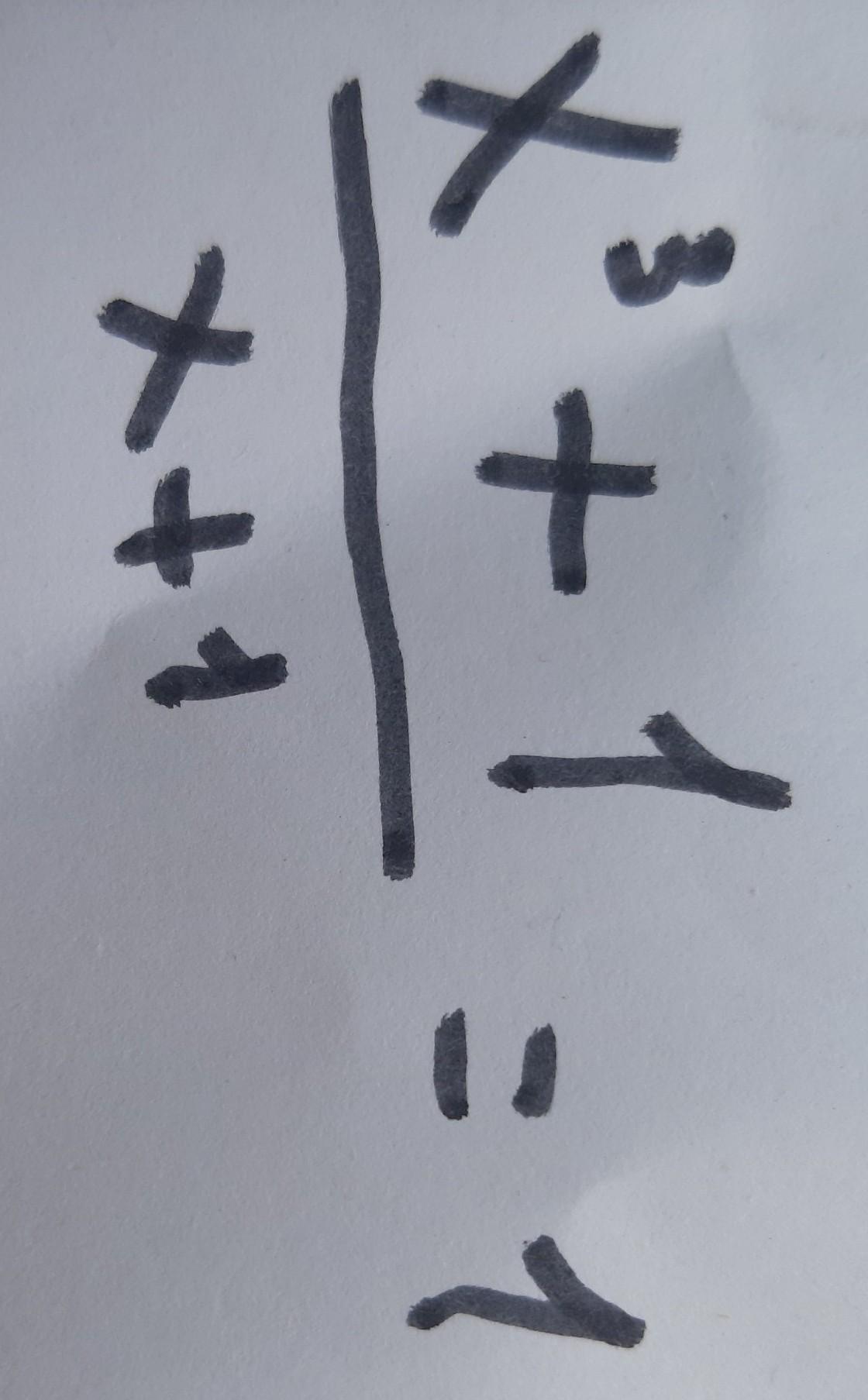Ответы
Ответ дал:
1
Так как знаменатель дроби не может равняться 0, записываем ОДЗ на х:
Теперь можем упростить дробь расписав числитель по формуле:
Тогда:
Оба корня входят в область допустимых значений, поэтому пишем ответ:
Ответ: 0, 1
SmallBrainMan:
Спасибо!
Обращайтесь)
Ответ дал:
1
Ответ:Вот решение
Объяснение:
Приложения:
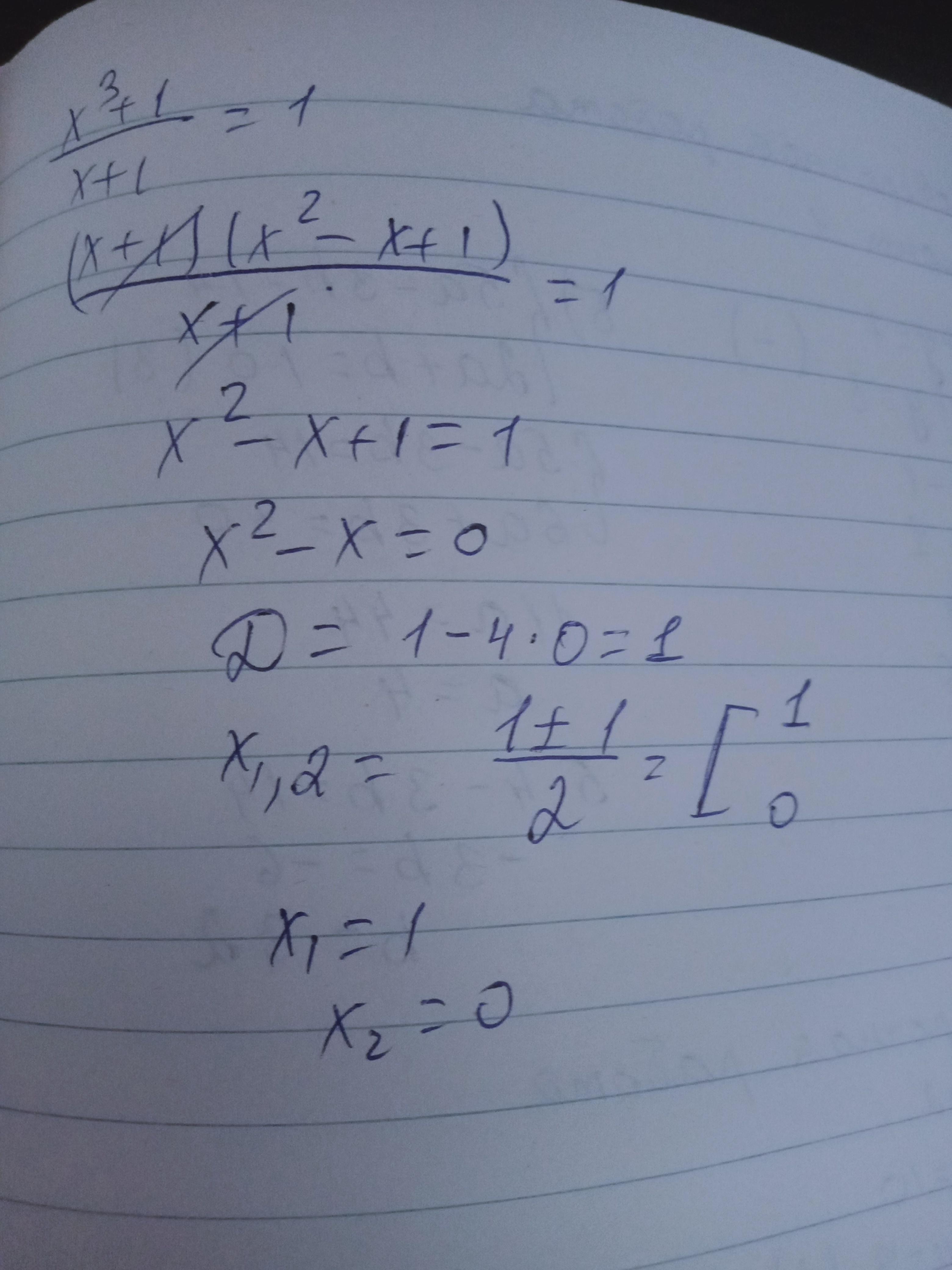
Спасибо!
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад