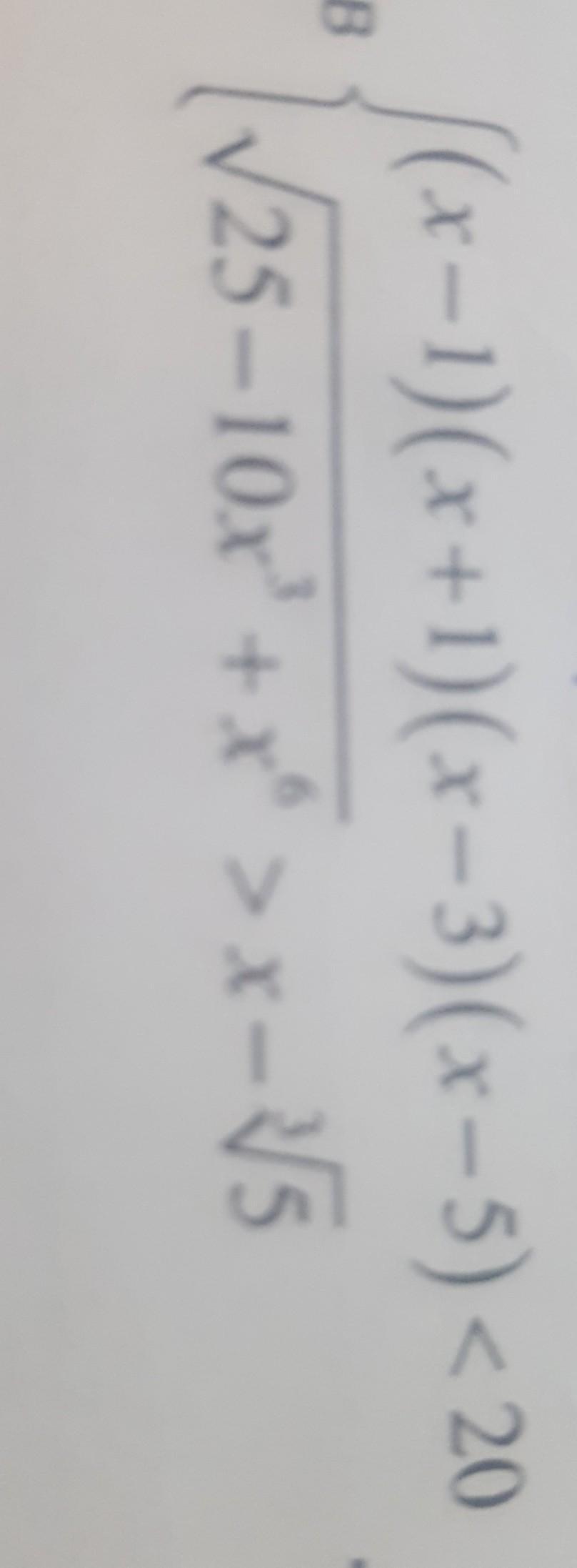Question

Решите данное неравенство.​

Answer 1

Разделим систему на 2 неравенства и решим каждое отдельно:

$(x-1)(x+1)(x-3)(x-5)<20\\(x^2-1)(x-3)(x-5)<20\\(x^3-3x^2-x+3)(x-5)<20\\x^4-5x^3-3x^3+15x^2-x^2+5x+3x-15<20\\x^4-8x^3+14x^2+8x-15-20<0\\x^4-4x^3-4x^3+5x^2+16x^2-7x^2-20x+28x-35<0\\x^2(x^2-4x+5)-4x(x^2-4x+5)-7(x^2-4x+5)<0\\(x^2-4x+5)(x^2-4x-7)<0\\PO TEOREME:\x^2-4x+5<0(1)\x^2-4x-7>0(2)\\x^2-4x+5>0(3)\x^2-4x-7<0(4)\\(1)=>xnotin R (x^2-4x+5>0)\(2)=>x^2-4x-7=0\\D=b^2-4ac=16+4*1*7=16+28=44\\x=frac{4pmsqrt{44}}{2} =2pmsqrt{11}$

$+++++(2-sqrt{11})-----(2+sqrt{11})+++++\\xin(-infty;2-sqrt{11})U(2+sqrt{11};+infty)\\(3)=>xin R\\(4)=>xin(2-sqrt{11};2+sqrt{11})\\(1)U(2)U(3)U(4)=>xin (2-sqrt{11};2+sqrt{11})\\\\sqrt{x^6-10x^3+25}>x-sqrt[3]{5} \\sqrt{(x^3+5)^2}>x-sqrt[3]{5}\\ mid x^3+5 mid+sqrt[3]{5}>x$

А сейчас подумаем: а когда такое может быть? Если слева у нас модуль, так ещё и + число, которое >0 , а слева просто x , то получается что это будет выполнятся всегда, так как при подстановке чисел <0 , у нас будет справа - а слева из-за модуля +

При подстановке чисел >0 , справа у нас будет всегда больше, так как число в кубе + положительные числа. Значит из второго уравнение x∈R

$OTBET:xin(2-sqrt{11};2+sqrt{11}})$