Question

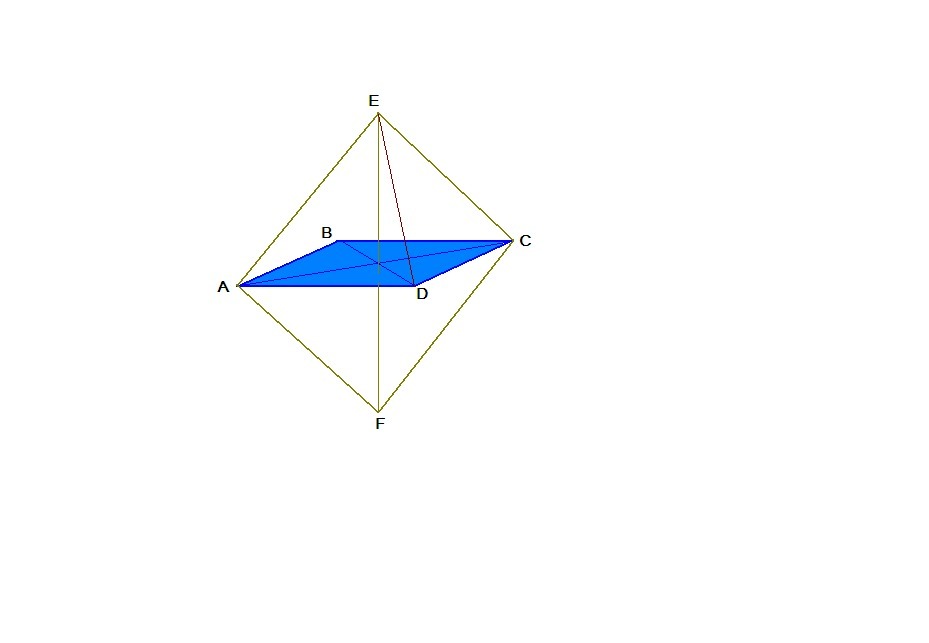
Квадраты ABCD  и AECF расположены так что BD перпендикулярно EF.

а) Доказать что прямая EF перпендикулярна к плоскости ABC

б)Найти угол между прямыми  АС и ЕD

 

Answer 1

а) По условию EF⊥BD, и EF⊥AC как диагонали квадрата AECF.
Прямая EF перпендикулярна двум пересекающимся прямым плоскости (АВС) ⇒ EF⊥(ABC).
б) АС⊥EF как диагонали квадрата AECF, АС⊥BD как диагонали квадрата ABCD, ⇒ АС⊥(EBD).
ED⊂(EBD) ⇒ AC⊥ED, т.е. угол между прямыми АС и ED равен 90°