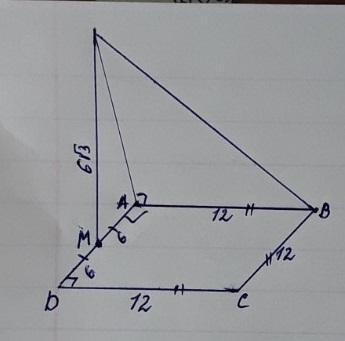
Даю 75 балів Через середину M сторони AD квадрата ABCD до його площини
проведений перпендикуляр MK завдовжки 6√3 см. Сторона квадрата
дорівнює 12 см. Обчисліть площу трикутника AKB.
Ответы
Ответ дал:
7
Через середину M стороны AD квадрата ABCD к его плоскости
проведен перпендикуляр MK длиной 6√3 см. Сторона квадрата
равен 12 см. Вычислите площадь треугольника AKB.
Объяснение:
ΔМАК-прямоугольный , т.к МК⊥(АВС). М-середина стороны квадрата ⇒МА=6 см. По т. Пифагора КА=√( МК²+МА²)=√(36*3+36)=12(см).
Т.к. проекция МА⊥АВ прямой лежащей в плоскости ( АВСD-квадрат), то и наклонная КА⊥АВ, по т. о 3-х перпендикулярах.
ΔАКВ-прямоугольный , S=1/2*a*h , S=1/2*АВ**КА=1/2*12*12=72( см²)
Приложения:
polina4124:
привет, помоги пожалуйста решить задачи по геометрии
Помогите кто-нибудь если сможете https://znanija.com/task/35819003
Вас заинтересует
1 год назад
1 год назад
3 года назад
8 лет назад