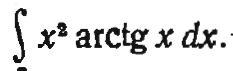Question

найти интеграл ////////////

Answer 1

$int {x}^{2} arctg(x)dx = I$

Применяем формулу интегрирования по частям (интегрируем х², дифференцируем аrctg(x)):

$I = frac{{x}^{3}}{3} arctg(x) - int frac{ {x}^{3} }{3} times frac{1}{1 + {x}^{2} }dx = frac{ {x}^{3} }{3} arctg(x) - \ - frac{1}{3} int frac{ {x}^{3} }{1 + {x}^{2} } dx$

Решим последний интеграл:

$int frac{ {x}^{3} }{ {x}^{2} + 1} dx = int frac{ {x}^{3} }{t + 1} times frac{1}{2x } dt = \ {x}^{2} = t rightarrow dx = frac{1}{2x} dt \ = frac{1}{2} int frac{t}{t + 1} dt = frac{1}{2} int 1 - frac{1}{t + 1} dt = \ frac{1}{2} t - frac{1}{2} int frac{1}{t + 1} dt = frac{t}{2} - frac{1}{2} int frac{1}{u} du = \ t + 1 = u rightarrow dt = du \ = frac{t}{2} - frac{1}{2} ln( |u| ) = frac{ {x}^{2} }{2} - frac{1}{2} ln( {x}^{2} + 1 )$

Подставляем:

$I = frac{ {x}^{3} }{3} arctg(x) - frac{1}{3} ( frac{ {x}^{2} }{2} - frac{1}{2} ln( {x}^{2} + 1) ) = \ = frac{ {x}^{3} }{3} arctg(x) - frac{ {x}^{2} }{6} + frac{1}{6} ln( {x}^{2} + 1) + C$

Answer 2

все правильно, только в ответе вместо хх^3/3, должно быть x^2arctgx/3