Question

Решить неравенство:
Cos2x + cosx ≥0

Answer 1

$cos2x + cos x geq 0$

$2cos^2x-1 + cos x geq 0$

$2cos^2x + cos x-1 geq 0$

Решим соответствующее квадратное уравнение:

$2cos^2x + cos x-1 =0$

$D=1^2-4cdot2cdot(-1)=9$

$cos x=dfrac{-1-3}{2cdot2} =-1$

$cos x=dfrac{-1+3}{2cdot2} =dfrac{1}{2}$

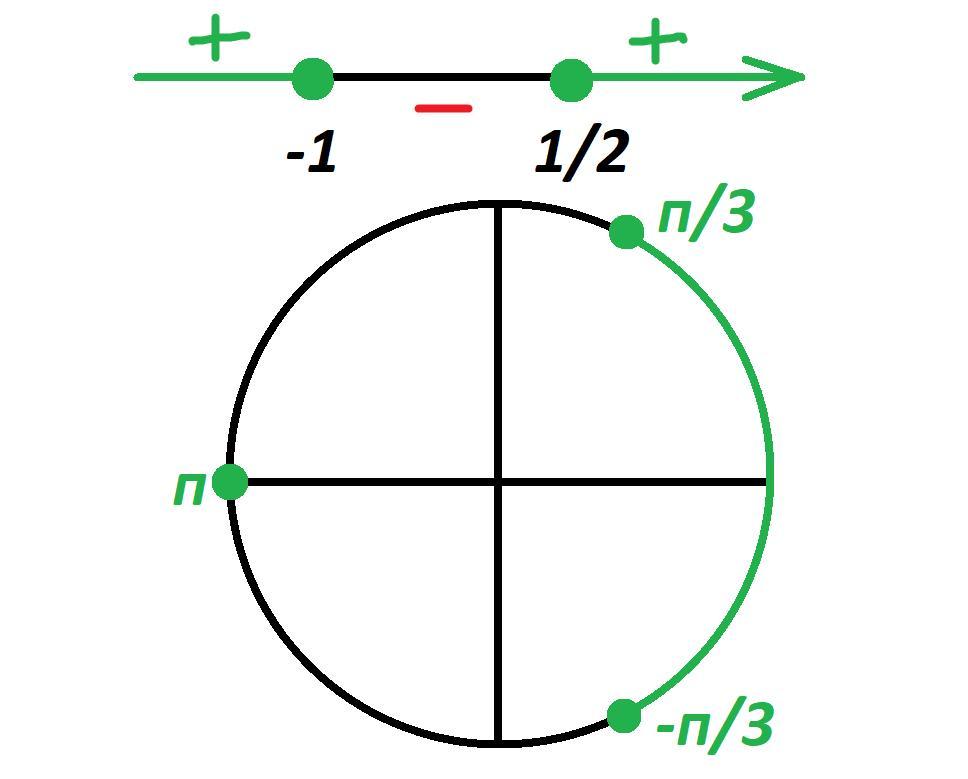
Дорешивая неравенство методом интервалов (картинка) получим:

$cos xinleft(-infty; -1right]cupleft[dfrac{1}{2}; +inftyright)$

Учитывая, что косинус не принимает значения, по модулю превышающие 1, получим:

$cos xinleft{-1right}cupleft[dfrac{1}{2}; 1right]$

Рассматривая условие на числовой окружности (картинка), получим:

$xin{pi+2pi n}cupleft[-dfrac{pi}{3}+2pi n ; dfrac{pi}{3}+2pi nright], ninmathbb{Z}$