Во вложении 444444444444444
Приложения:
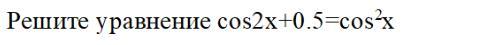
oganesbagoyan:
cos2x +1/2 = (1+cos2x)/2 ⇒ cos2x=0 ; 2x = π /2 +πk /2
Как способ называется ?
≈ Формулы понижения степени в тригонометрии
cos2α =cos²α -sin²α =cos²α -(1-cos²α) =2cos²α -1 ⇒cos²α =(1+cos2α)/2
Спасибо
cos2α =1 -2sin²α⇒sin²α =(1- cos2α)/2 ; sin⁴α =(sin²α)² =((1 -cos2α)/2)² и т.д
Ответы
Ответ дал:
3
Запишем в виде:
Ответ: , k∈Z или
, k∈Z
5 поставили спс :*
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад