Question

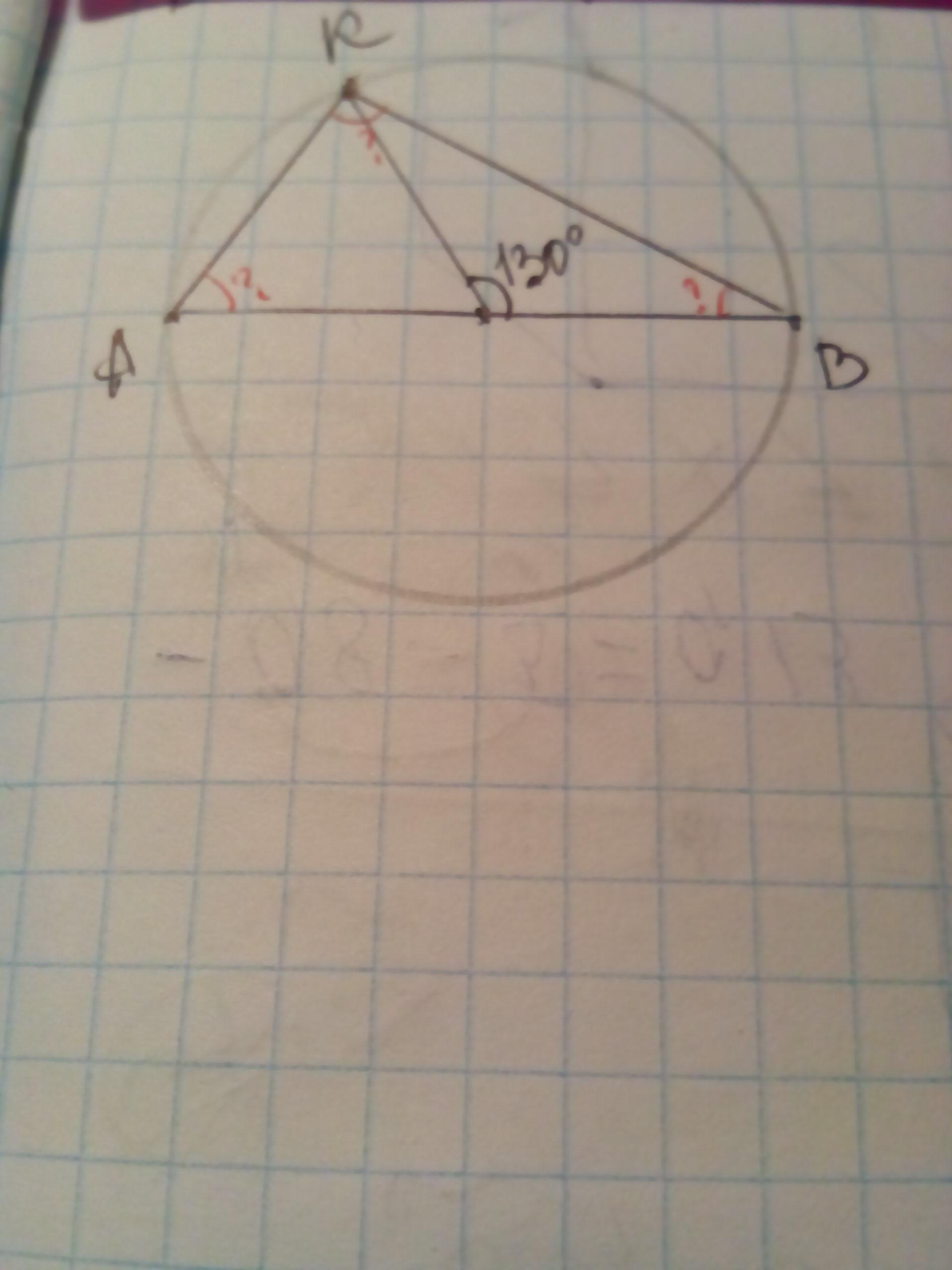
у колі із центром О проведено діаметр АВ і хорди АК і КВ . Знайти кути трикутника АКВ якщо КОВ=130

Answer 1

Ответ:

90*

Объяснение:

Центр окружности  - т.О.

Из ΔАКО ( тр-ник равнобедренный АО=ОК - как радиусы одной окружности) ∠КОВ=130° - это внешний угол ΔАКО⇒

∠А=∠АКО=130:2=65°

Из ΔОКВ (тр-ник равнобедренный ОК=ОВ как радиусы⇒∠В=∠ОКВ=(180-130):2=25°

∠АКВ=∠АКО+∠ОКВ=25+65=90°

Ответ: ∠А=65°,∠В=25°,∠К=90°