Пусть  и
и  окружности, касающиеся внутренним образом, радиусы -
окружности, касающиеся внутренним образом, радиусы -  и
и  соответственно, причем
соответственно, причем  ,
,  - точка касания.
- точка касания.
Рассмотрим такое множество точек  , что, во-первых,
, что, во-первых,  , а во-вторых, любой центр окружности, касающейся окружностей
, а во-вторых, любой центр окружности, касающейся окружностей  и
и  (первой - внешним образом, второй - внутренним), принадлежит
(первой - внешним образом, второй - внутренним), принадлежит  .
.
Найдите площадь фигуры, ограниченной  .
.
Ответы
Ответ дал:
0
Ответ:
Объяснение:
см. приложение
Приложения:

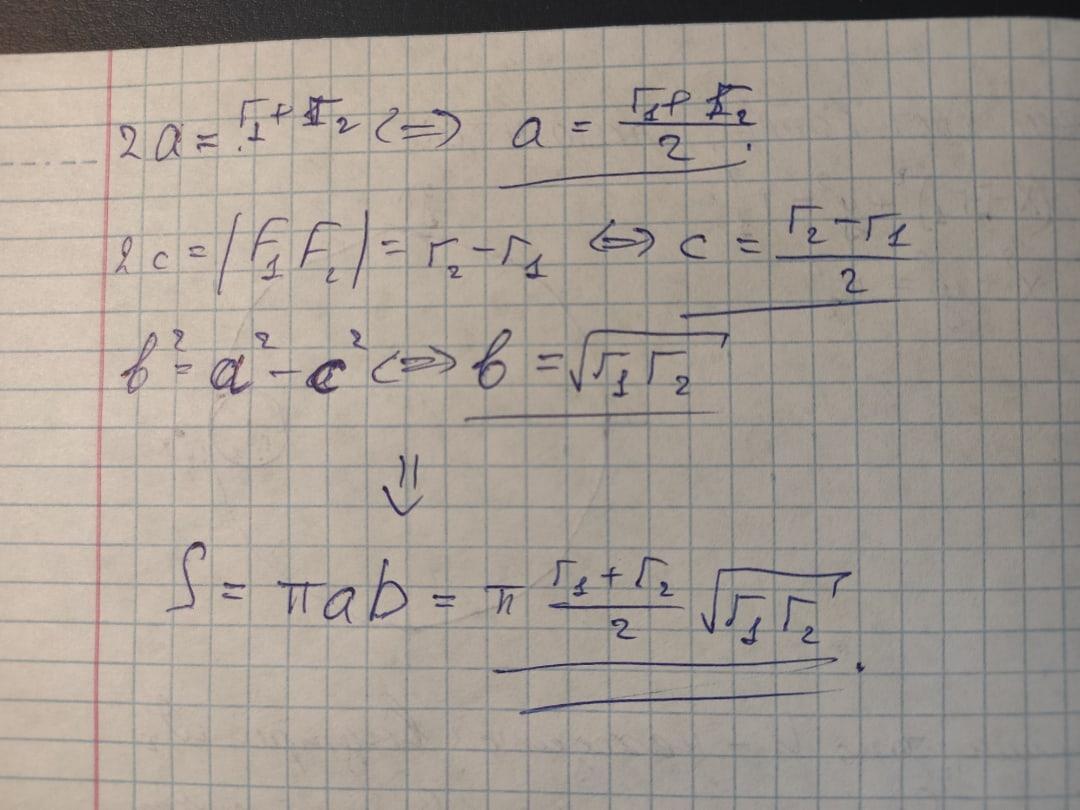
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад