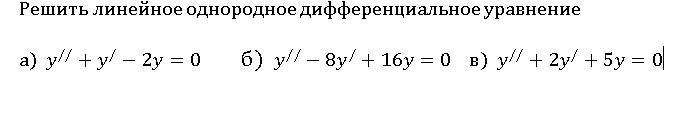Question

Решить линейное однородное дифференциальное уравнение

Answer 1

Ответ:

y"+y'-2y=0

Производим замену:

y"=$k^{2}$ ; y'=k ; y=1

$k^{2}$+k-2=0

находим дискриминант: a=1, b=1,c=-2

D=$b^{2}$-4ac=1-4*1*(-2)= 1+8=9

$sqrt{D$=3

Находим корни k1 и k2

$k1=frac{-1-3}{2*1} = -2\\k2=frac{-1+3}{2*1}= 1$

Обратная замена:

y1 = $e^{-2x}$

y2 =$e^{x}$

Общее решение однородного уравнения имеет вид:

y=C1y1+C2y2