Вычислить неопределенные интегралы, используя замену переменной и
проверить дифференцированием:
Приложения:
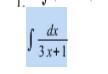
Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
Вас заинтересует
1 год назад
1 год назад
1 год назад
8 лет назад