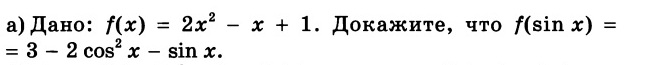Ответы
Ответ дал:
0
подставляем в f(x) вместо x выражение sinx, тогда
f(sinx)=2*(sinx)^2-sinx+1. Пользуемся основным тригонометрическим тождеством, что sin^2+cos^2=1, отсюда sin^2=1-cos^2
Значит, f(sinx)=2*(sinx)^2-sinx+1
f(sinx)=2*(1-(cosx)^2)-sinx+1
f(sinx)=2-2(cosx)^2-sinx+1
f(sinx)=3-2(cosx)^2-sinx
f(sinx)=2*(sinx)^2-sinx+1. Пользуемся основным тригонометрическим тождеством, что sin^2+cos^2=1, отсюда sin^2=1-cos^2
Значит, f(sinx)=2*(sinx)^2-sinx+1
f(sinx)=2*(1-(cosx)^2)-sinx+1
f(sinx)=2-2(cosx)^2-sinx+1
f(sinx)=3-2(cosx)^2-sinx
Вас заинтересует
2 года назад
8 лет назад
10 лет назад
10 лет назад
11 лет назад