Question

найдите значение параметра а , при котором касательная к графику функции
$y = x^{3} + a{x}^{2} - a$
в точке х=-1 проходит через току М(1;7)​

Answer 1

Производная равна y' = 3x² + a².

В точке х = -1 она равна y' = 3 + a².

Функция в точке х = -1 равна -1 - а² - а.

Составляем уравнение касательной в точке х = -1.

у(кас) = (3 + a²)(х + 1) + (-1 - а² - а) = 3х + а²х - а + 2.

Подставляем координаты точки М (1; 7).

7 = 3 + а² - а + 2.

Получаем квадратное уравнение а² - а - 2 = 0.   Д = 1 + 8 = 9.

а1 = (1 + 3)/2 = 2,  а2 = (1 - 3)/2 = -1.

Ответ: а1 = 2, а2 = -1.

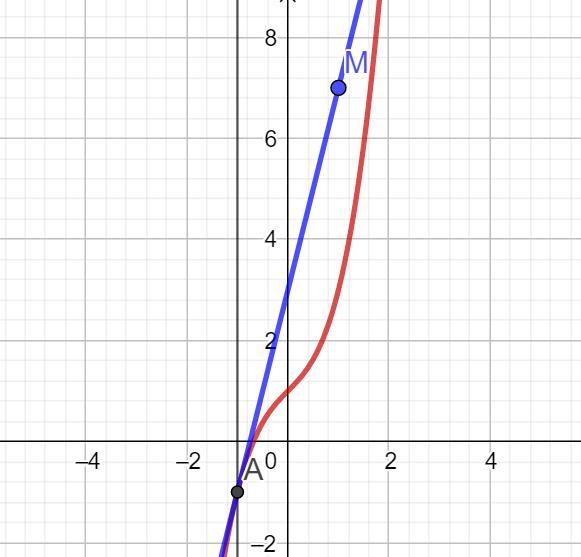
Для второго варианта есть график.