Помогите пожалуйста. Докажите, что F(x)=x * кубический корень на x - sin2x + 3 если первообразная для функции f(x) = 4/3 кубический корень на x - 2 cos2x на (0 ; +∞).
Приложения:
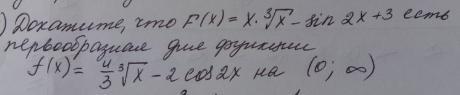
Ответы
Ответ дал:
0
Ответ дал:
0
Если производная F'(x)=f(x) на указанном промежутке, то утверждение будет доказано.
Найдем производную( х*∛х-sin2x+3)'=(x⁴/³-sin2x+3)'=
4(x¹/³)/3-2cos2x+0=4∛x/3-2cos2x
Требуемое доказано.
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад