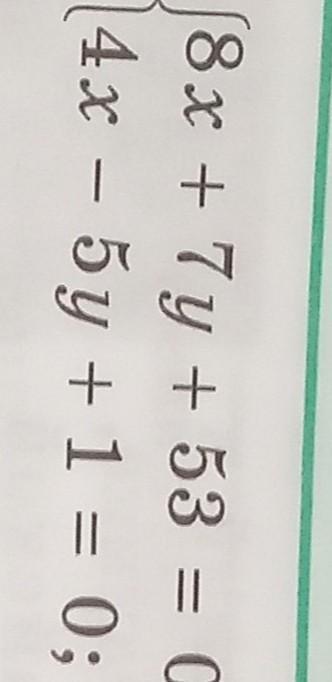Ответы
Ответ дал:
1
Решить систему уравнений:
Ответ: x = −4; y = −3.
sonehka6878:
Спасибо огромное
Ответ дал:
0
Ответ:x = -4,y = -3
Пошаговое объяснение:
Решим задачу методом постановки.Выразим у в первом уравнении
7y = -8x-53=> y = -8x-53/7.Подставляем полученное выражение во второе уравнение 4x - 5*(-8x-53/7)+1=0.Домножим уравнение на 7, чтобы избавиться от дроби и раскрываем скобки .Получается 28x+40x+265+7=0, 68x+272=0, 68x= -272, x = -4.Подставляем X в -8x-53/7,
-8*-4-53/7 =-3
7y = -8x-53
y = -8x-53/7
4x - 5*(-8x-53/7)+1=0 * 7
28x+40x+265+7=0
68x+272=0
68x= -272
X = -4
-8*-4-53/7 =-3
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад