Найдите площадь равнобедренного треугольника, вписанного в окружность радиуса 17 см и высотой, проведённой к основанию, равной 25 см. Ответ дайте в квадратных сантиметрах.
Ответы
Ответ дал:
23
Ответ: 375 см²
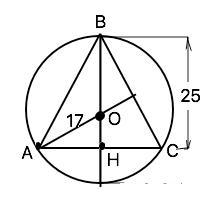
Объяснение: Центром окружности, описанной около треугольника, является точка пересечения срединных перпендикуляров. Следовательно, центр О находится на высоте ВН треугольника АВС, которая является и срединным перпендикуляром. ( см. рисунок).
АО=ВО - радиусы и равны 17 см. Тогда ОН=ВН-ВО=25-17=8 (см).
Из ∆ АОН по т.Пифагора АН=15 (см).
АН=НС.
АС=2•АН=30 (см).
Ѕ (АВС)=ВН•АС:2=25•15=375 см²
Приложения:
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад