Question

Основание равнобедренного треугольника 16 см ,высота спущенное на основание 4 см , найти радиус описанной около неё окружности

Answer 1

Ответ:

$frac{5}{8}$ см

Пошаговое объяснение:

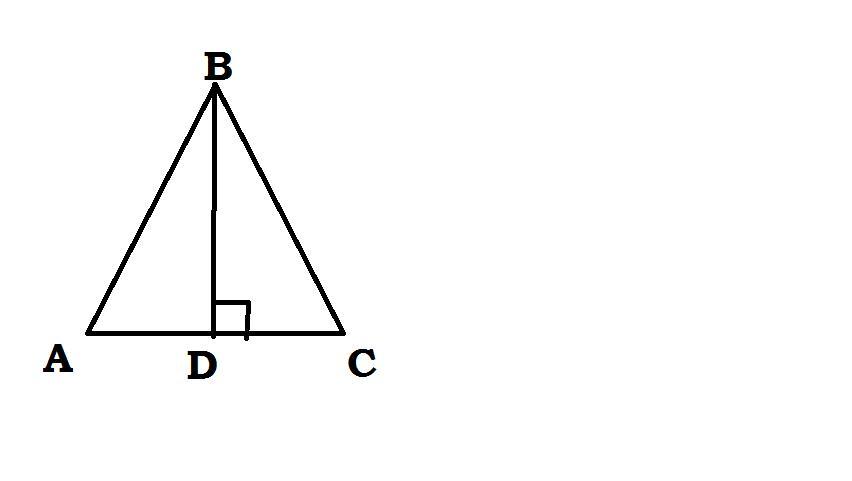
Так как треугольник АВС равнобедренный, ВД - его высота, медиана и биссектриса, значит АД=СД=16:2=8 см

Рассмотрим треугольник ВДА:

угол ВДА = 90 градусов

По теореме Пифагора

АВ=-ВС=$sqrt{8^{2} +4^{2} } =sqrt{80} =4sqrt{5}$ см

Радиус описаной окружности равен

R=$frac{abc}{4S}$

Sтреугольника=$frac{1}{2}$×ВД×АС=

R=($4sqrt{5}$ ×