Question

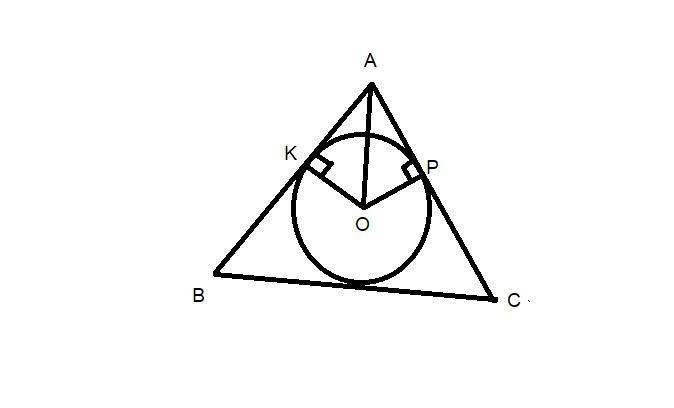
В треугольник АВС вписана окружность с центром О. Из точки О к сторонам АВ и АС треугольника проведены перпендикуляры ОК и ОР. Докажите, что АК=АР.

Answer 1

Прямоугольные треугольники равны по гипотенузе и катету

OK=OP=R

OA-общая, значит равная

AK⊥OK и AP⊥OP так как касательные перпендикулярны радиусу вписанной окружности

Из равенства треугольников следует равенство соответствующих катетов AK=AP в этих треугольниках