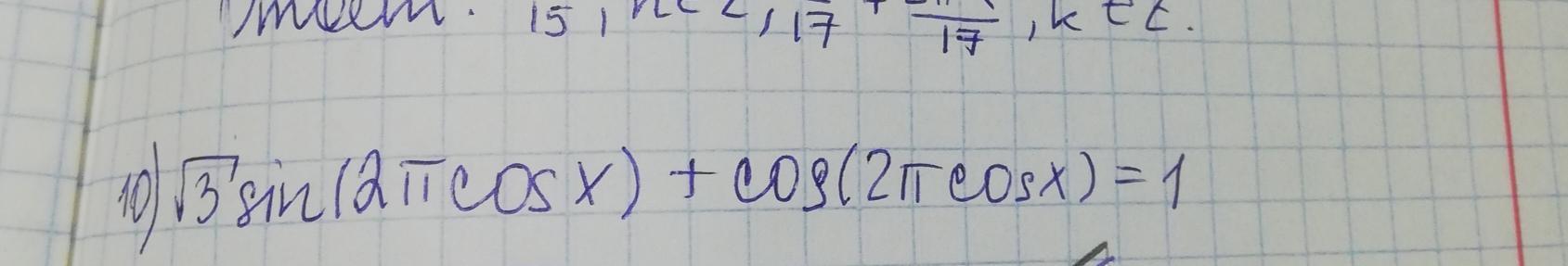Question

ПОМОГИТЕ РЕШИТЬ!!!!
Тригонометрическое уравнение

Answer 1

√3 ·sin(2πcosx)+cos(2πcosx)=1 |:2

(√3)/2 ·sin(2πcosx)+(1/2)cos(2πcosx)=1/2

Вспомним, что сos(π/6)=(√3)/2, а sin(π/6)=1/2. Тогда можно переписать равенство:

sin(2πcosx)·сos(π/6)+cos(2πcosx)·sin(π/6)=1/2

По формуле синуса суммы, получим:

sin(2πcosx+(π/6))=1/2

Откуда

$displaystyle 2pi cos x+frac{pi}6=(-1)^ncdot frac{pi}6+pi n, nin mathbb{Z}\ \ cos x=frac{(-1)^n-1+6n}{12} ,nin mathbb{Z}$

|cosx|≤1, поэтому подходят только n={-2;-1;0;1;2}

Соответственно cosx = {-1;-2/3;0;2/3;1}

Решая простейшие тригонометрические уравнения НА ТРИГОНОМЕТРИЧЕСКОМ КРУГЕ, запишем красивый ответ для x.

$begin{bmatrix}displaystyle x=frac{pi}2kqquad qquad quad \ displaystyle x=pm arccos{frac23 }+pi kend{matrix} kin mathbb{Z}$

Формально стоил ввести 5 переменных для каждого значения cosx т.к. все значения не зависит друг от друга. Но тогда ответ был бы громоздким. К тому же если рассматривать всё множество действительных чисел, то я указал все решения уравнения.